實際熱機中，有些過程工質的狀態參數p、v、T 等都有顯著的變化，與外界之間換熱量也不可忽略不計，這時它們不能簡化為四種基本的熱力學過程(定容、定壓、定溫和絕熱)。試驗測定了一些過程中1kg 工質的壓力p 和v 的關系，發現它們接近指數函數，用數學表達式描述即：p*vn=定值。該式即多變過程的過程方程式。n 為多變指數，它可以是負無窮到正無窮之間的任意數值。多變過程比前述幾種特殊過程更為一般化，但也并非任意的過程，它仍根據一定的規律變化：整個過程服從過程方程p*vN=定值，n 為某一定值。

　　實際過程往往更為復雜。譬如柴油機氣缸中的壓縮過程，開始時工質溫度低于缸壁溫度，邊吸熱邊壓縮而溫度升高，高于缸壁溫度后則邊壓縮邊放熱，整個過程n 大約從1.6 變化到1.2 左右;至于膨脹過程，由于存在后燃及高溫時被離解氣體的復合放熱現象，情況更為復雜，其散熱規律的研究已不屬于熱力學的范圍。對于多變指數n 式變化的實際過程，若n 的變化范圍不大，則可用一個不變的平均值近似地代替實際變化地n;若n 地變化較大，則可將實際過程分成數段，每一段都近似為n 值不變。

　　本課題中，由于n 值的變化范圍不大，根據以往實際工況和以往經驗，選取n=1.3。

　　如圖3 所示，壓縮和膨脹為多變過程，多變指數n=1.3。膨脹結束點A 的壓力應小于吸氣壓力Ps，壓縮結束點B 的壓力應大于排氣壓力Pd，但考慮影響有限，故膨脹結束點A 的壓力=Ps，壓縮結束點B 的壓力=Pd。

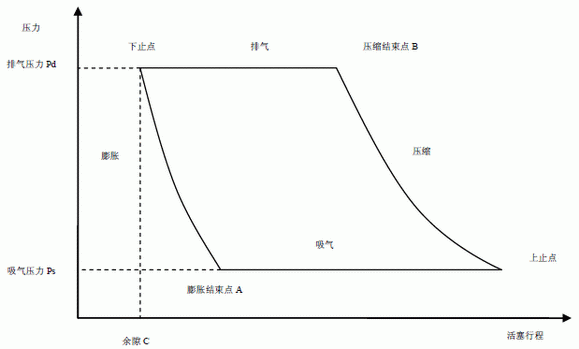
　　圖 3 壓縮機整個行程中的P-V 關系

　　4.4.4 活塞頂部壓力在運動分析中的體現：

　　4.4.4.1 MSC.ADAMS 中IF 函數的定義

　　IF(expr1：expr2，expr3，expr4)

　　式中，expr1 為控制變量，expr2，expr3 和expr4 均為表達式。

　　函數F=IF(expr1：expr2，expr3，expr4)的含義為：

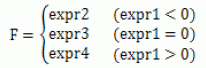
　　4.4.4.2 在本課題中IF 語句算法

　　圖4 所示為本課題中壓縮機活塞端面受力IF 語句算法。先由活塞的速度方向(大于零/小于零)，判斷活塞運動處于吸氣/膨脹狀態，還是壓縮/排氣狀態，再根據活塞質心位置與膨脹結束點的關系確定是吸氣狀態還是膨脹狀態;根據活塞質心位置與壓縮結束點關系確定是壓縮狀態還是排氣狀態。

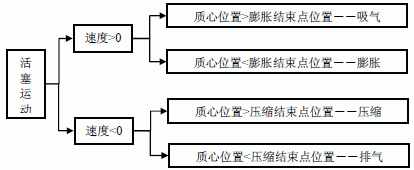
　　圖4 活塞端面受力IF 語句算法

　　程序框圖如圖5 所示：

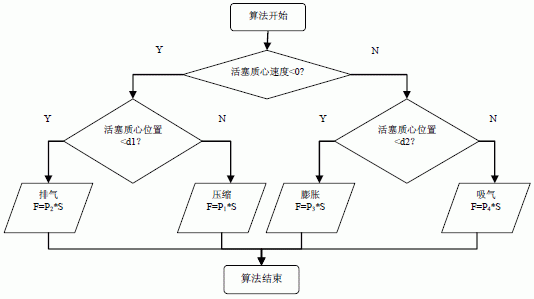
　　圖5 活塞端面受力IF 語句程序框圖

　　4.4.4.3 If 語句公式

　　將在UG 中建好的模型導入ADAMS 后，根據實際情況施加所需的運動約束。設定End Time = 10，step = 100，進行初步動態運行，測量所得數據。根據上述數據經過計算，得出在三種不同工況下，活塞的排氣點d1，吸氣點d2 的位置，如表5 所示。

　　表5 壓縮機活塞行程參數(2)

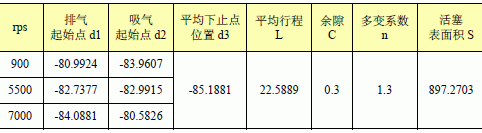
　　以活塞3 在工況900rps 下端面受力為例：吸氣壓力Ps=0.358MPa, 排氣壓力Pd=2.97MPa, 排氣起始點位置d1=-80.9924, 吸氣起始點位置d2=-83.9607,活塞平均下止點位置d3=-85.1881, 活塞表面積S=897.2703, 活塞平均行程L=22.5889,余隙C=0.3,多變系數n=1.3。

　　900r/min：

　　Piston_3 氣體方程：

　　IF( VZ(piston3.cm):

　　IF(.5H11G.cm_dis3+80.9924:897.2703*2.97,897.2703*2.97,897.2703*0.358*((22.5889+0.3)/( .5H11G.cm_dis3+85.1881+0.3))**1.3),

　　IF(.5H11G.cm_dis3+80.9924:897.2703* 0.358, 897.2703*2.97, 897.2703 *2.97),

　　IF(.5H11G.cm_dis3+83.9607:897.2703*2.97*(0.3/(.5H11G.cm_dis3+85.1881+0.3))**1.3, 897.2703*0.358, 897.2703*0.358)

　　)

　　在模型上施加運動學約束以及力約束后，進行900rps 的運動仿真，以活塞3 為例，摘取其位移、速度、加速度與受力的曲線圖，根據先前算出的d1、d2 位置，判定活塞在整個行程中的四個階段的狀態。一個周期內壓縮機進行膨脹——吸氣——壓縮——排氣為一次完整循環。狀態判定結果如圖6 所示。

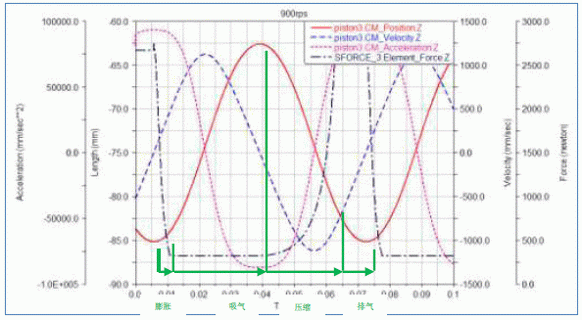
　　圖6 位移、速度、加速度與受力的曲線圖