3.1 測(cè)量數(shù)據(jù)的濾波處理

　　該測(cè)量?jī)x是數(shù)據(jù)更新率較高的實(shí)時(shí)系統(tǒng)，為克服采集系統(tǒng)采集數(shù)據(jù)時(shí)隨機(jī)干擾帶來(lái)的誤差，軟件上對(duì)測(cè)得的數(shù)據(jù)進(jìn)行了數(shù)字濾波，鑒于滑動(dòng)平均濾波算法具有能夠良好抑制周期性干擾，平滑度高的特點(diǎn)，這里選取滑動(dòng)平均濾波法。其原理是：將測(cè)量數(shù)據(jù)看成一個(gè)長(zhǎng)度為N的隊(duì)列，把每次的采樣新值放人隊(duì)尾，隊(duì)首的一個(gè)數(shù)據(jù)出列，其他數(shù)據(jù)前移一位，這樣隊(duì)列中始終有N個(gè)“最新”數(shù)據(jù)，再將隊(duì)列中的N個(gè)數(shù)據(jù)進(jìn)行數(shù)學(xué)平均，從而得到新的濾波值。其數(shù)學(xué)表達(dá)式為：

?

　　式中：

為第n次采樣濾波后的輸出;Xn-i為未經(jīng)濾波的第n-i次采樣;N為滑動(dòng)平均項(xiàng)數(shù)。

?

　　數(shù)據(jù)采集過(guò)程如下：按測(cè)量鍵后，連續(xù)采樣1 min(1 min采樣10次)，此次測(cè)量顯示這一分鐘內(nèi)采樣值的平均值，繼續(xù)采樣，此時(shí)顯示值為此次采樣值與前九次采樣值的平均值，即每6 s得一個(gè)數(shù)據(jù)值，LCD可以連續(xù)顯示。當(dāng)切換測(cè)量擋時(shí)，延時(shí)采樣0.5s。

　　3.2 PID控制系統(tǒng)

　　為防止調(diào)節(jié)傳感器接收靈敏度時(shí)由于超調(diào)或者失調(diào)引起的振蕩，使儀器讀數(shù)能夠平緩上升或者下降，這里采用PID算法加以調(diào)節(jié)，以對(duì)振蕩進(jìn)行抑制，在控制過(guò)程中采用智能判斷的方法使系統(tǒng)處于最優(yōu)狀態(tài)。PID調(diào)節(jié)器具有規(guī)律簡(jiǎn)單，運(yùn)行可靠，易于實(shí)現(xiàn)等特點(diǎn)。

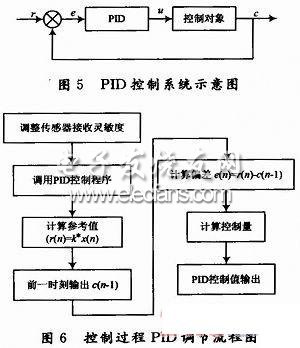
　　圖5是PID控制的基本原理示意圖，其基本輸入輸出關(guān)系可表示為：

?

　　式中：μ(t)為控制器輸出;e(t)為控制器輸入的偏差信號(hào);e(t)=r(t)-c(t)。

?

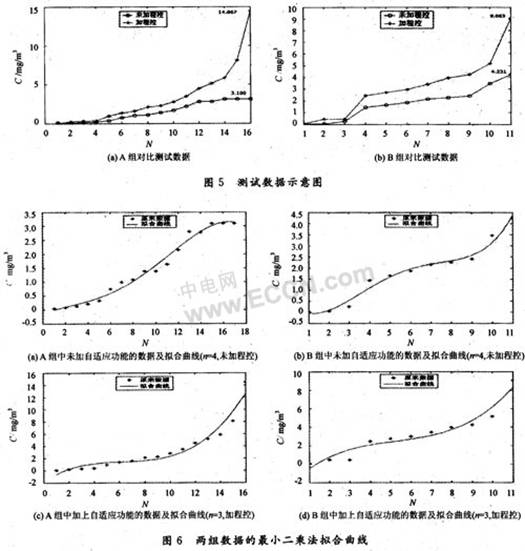
　　比例環(huán)節(jié)調(diào)整系統(tǒng)的開(kāi)環(huán)比例系數(shù)，提高系統(tǒng)的穩(wěn)態(tài)精度，降低系統(tǒng)的惰性，加快響應(yīng)速度;積分環(huán)節(jié)可以提高系統(tǒng)的型別，消除或減小穩(wěn)態(tài)誤差，使系統(tǒng)的穩(wěn)態(tài)性能得到改善;微分控制使得系統(tǒng)的響應(yīng)速度變快，超調(diào)減小，振蕩減輕。PID控制過(guò)程調(diào)節(jié)流程如圖6所示。

　　3.3 PID參數(shù)的設(shè)定

　　PID控制參數(shù)的設(shè)定是控制系統(tǒng)設(shè)計(jì)的核心內(nèi)容，它是根據(jù)被控對(duì)象的特性確定PID控制器的比例系數(shù)、積分時(shí)間和微分時(shí)間的大小，確保其在系統(tǒng)受到擾動(dòng)后仍保持穩(wěn)定并將誤差保持在最小值。

　　3.3.1 PID參數(shù)的初始值

　　Ziegler Nichols方法是基于簡(jiǎn)單被控過(guò)程的Niquist曲線(xiàn)的臨界點(diǎn)計(jì)算PID參數(shù)初值，其整定準(zhǔn)則是要求系統(tǒng)的暫態(tài)過(guò)程衰減率為0.75，該算法簡(jiǎn)單，使用方便。本文采用4：1的衰減比性能準(zhǔn)則獲得PID參數(shù)的初始值。

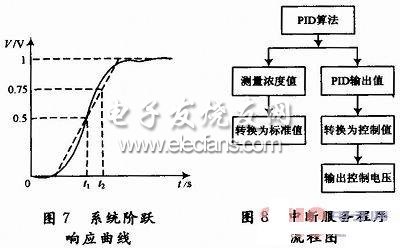
　　設(shè)控制系統(tǒng)有一響應(yīng)曲線(xiàn)，如圖7所示，給系統(tǒng)加一階躍輸入U(xiǎn)，可用一階延時(shí)系統(tǒng)近似為：

?

　　式中：K為放大系數(shù);τ為滯后時(shí)間;T為時(shí)間常數(shù)。

　　設(shè)輸出值達(dá)到設(shè)定值的50%和75%時(shí)所用的時(shí)間分別為：t1和t2，則PID參數(shù)的初始值可表示為比例系數(shù)Kp=1.2U/(RL)，積分時(shí)間常數(shù)TI=2L，微分時(shí)間常數(shù)TD=0.5L。其中：斜率R=(0.75-0.5)V/(t2-t1)，滯后L=t1-(2V0-4V1)(t2-t1)/V。

?