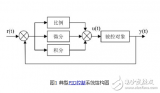
PID控制器的數(shù)學(xué)模型

　　在標(biāo)準(zhǔn)的控制類書籍上PID算法是這么定義的：

　　這個(gè)公式是連續(xù)系統(tǒng)用的，我們單片機(jī)的控制是用不了的，我們的單片機(jī)使用的是離散的控制模型也叫0階保持器的離散系統(tǒng)，就是需要把上面的公式離散化，而這個(gè)離散化的過程我們使用的是后項(xiàng)差分法。首先把上面的積分傳遞函數(shù)轉(zhuǎn)化為連續(xù)的s域模型：

　　使用后向差分法可以得到s域到z域的映射關(guān)系：

　　于是可以得到：

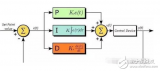
　　這里特地給出了Kp Ki Kd這三個(gè)參數(shù)，這三個(gè)參數(shù)就是大家最常看到的那個(gè)離散的PID公式，也就是說你在這里既可以使用Kp Ti Td的參數(shù)來建模也可以使用Kp Ki Kd的參數(shù)來建模，到這里就總算是可以把我們的傳遞函數(shù)放在系統(tǒng)中用自控原理的相應(yīng)工具來分析了。分析之前要先聲明一個(gè)事情，有人發(fā)現(xiàn)（比如在MWC和其他許多飛控中）用陀螺儀的輸出來當(dāng)做PID中的微分項(xiàng)，會(huì)取得比標(biāo)準(zhǔn)PID更好的控制效果，乍一看這么做與用前后兩次歐拉角作差沒有區(qū)別（因?yàn)榻撬俣日镁褪墙嵌鹊奈⒎郑刂菩Ч灰粯泳驼f不通了。

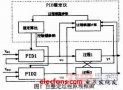
　　其實(shí)是這個(gè)樣子的，如果我們?cè)诔绦蛑凶隽朔浅：玫木€程安全的處理并且控制頻率和姿態(tài)解算讀陀螺的頻率是一樣的的情況下二者確實(shí)是沒有任何差別的，但是大家的飛控都寫的非常簡(jiǎn)單，姿態(tài)解算頻率都高于控制頻率，于是讀到的陀螺儀的數(shù)據(jù)并不是‘當(dāng)前使用的姿態(tài)前一時(shí)刻’的數(shù)據(jù)而是‘后一時(shí)刻’的數(shù)據(jù)，這時(shí)候PID控制的微分部分就不再是‘后項(xiàng)差分’而是‘前向差分’了（這就是我前面要強(qiáng)調(diào)使用后項(xiàng)差分法的原因），那這個(gè)時(shí)候就尷尬了，我們不能全部使用前向差分模型來建模（因?yàn)榉e分還是使用的后向模型）兩邊分開用又會(huì)出現(xiàn)模型階次不匹配的問題，所以這時(shí)候是無法使用PID模型來考慮接下來的問題的，你使用的其實(shí)是兩個(gè)獨(dú)立的控制器并聯(lián)，一個(gè)是角度的PI控制器，而另一個(gè)是角速度的P控制器，二者采樣時(shí)間不一樣，于是得當(dāng)做兩個(gè)獨(dú)立的控制回路調(diào)整參數(shù)，這是使用這種控制器時(shí)的參數(shù)調(diào)整方法。也就道出了為什么部分情況下使用角度微分和角速度控制效果不一樣的問題，這種方法固然是很好的（可以有效的降低振動(dòng)），當(dāng)然前提是你按照二者獨(dú)立控制的思路來設(shè)計(jì)參數(shù)。但是很不幸，大家都沒有這么做，依然是把整體作為PID控制器來考慮，那么，我只能說這是個(gè)近似的PID控制器了，手調(diào)固然可以（萬能的實(shí)驗(yàn)調(diào)參啊）但是通過建模的方式算出優(yōu)化的參數(shù)就不可能了。我們接下來看會(huì)怎樣：

　　從系統(tǒng)的零極點(diǎn)圖理解PID控制的原理

　　有了上面的PID傳遞函數(shù)的離散系統(tǒng)模型我們就可以開始下一步了，將上面的分式上下做因式分解可以得到系統(tǒng)的零極點(diǎn)，在自控原理中我們知道，系統(tǒng)的極點(diǎn)確定系統(tǒng)的穩(wěn)定性情況，零點(diǎn)不影響系統(tǒng)穩(wěn)定性，零點(diǎn)和極點(diǎn)共同決定系統(tǒng)的響應(yīng)。這里說的有些模糊，在現(xiàn)代控制理論中會(huì)提到一種控制器叫零極點(diǎn)配置控制器，能更好的闡述零點(diǎn)的作用：系統(tǒng)中的零點(diǎn)可以用來與系統(tǒng)中的不穩(wěn)定（或者不想要）的極點(diǎn)對(duì)消來設(shè)計(jì)出理想的控制器（數(shù)學(xué)上），工程中我們考慮的是讓零點(diǎn)與我們不想要的極點(diǎn)盡可能的靠近，就能削弱這個(gè)不想要的極點(diǎn)對(duì)系統(tǒng)的影響。下面我們用極點(diǎn)配置的方法來設(shè)計(jì)PID控制器，這里提前聲明我們使用的并不是最標(biāo)準(zhǔn)的閉環(huán)極點(diǎn)配置方法，因?yàn)槲覀兊腜ID控制器只有兩個(gè)零點(diǎn)可以配置（如果使用PI控制器的話就只有一個(gè)零點(diǎn)可以自由配置了）而且還多了一個(gè)臨界穩(wěn)定的極點(diǎn)，反饋又使用的是單位負(fù)反饋……極大的限制了極點(diǎn)配置的自由度，于是我們?yōu)榱撕?jiǎn)單起見僅從開環(huán)部分進(jìn)行極點(diǎn)配置，這么做有許多不嚴(yán)謹(jǐn)?shù)牡胤剑菚?huì)簡(jiǎn)化許多工程上的應(yīng)用（在做自適應(yīng)PID控制器的時(shí)候會(huì)用到完整的極點(diǎn)配置方法，到那里就會(huì)發(fā)現(xiàn)是多么復(fù)雜的一件事兒了……）。

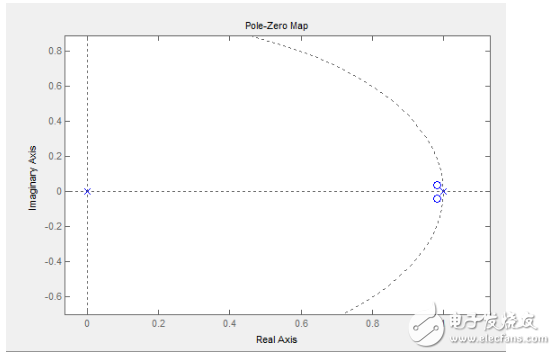
　　上圖是PID控制器開環(huán)部分（就是上面推導(dǎo)的數(shù)學(xué)模型）常見的零極點(diǎn)分布情況，有兩個(gè)固定在（0，0）和（1，0）位置的極點(diǎn)，兩個(gè)對(duì)稱分布的零點(diǎn)（手調(diào)參數(shù)時(shí)很難出現(xiàn)兩個(gè)零點(diǎn)都在實(shí)軸上的情況而且我們也不希望那樣），這兩個(gè)零點(diǎn)的位置是可調(diào)的，微分時(shí)間常數(shù)Td主管零點(diǎn)位置的左右移（注意是‘主管’，也就是說對(duì)虛軸的位置還是有影響的），常數(shù)越大越靠右（也就是說臨界穩(wěn)定極點(diǎn)的影響越弱，抗噪聲性能越好但到達(dá)0誤差的穩(wěn)態(tài)也就越困難，因?yàn)檫@個(gè)臨界穩(wěn)定的極點(diǎn)是在閉環(huán)系統(tǒng)中讓系統(tǒng)到達(dá)穩(wěn)態(tài)0誤差的關(guān)鍵但很影響穩(wěn)定性），積分常數(shù)Ti越大零點(diǎn)越靠近實(shí)軸，Ti在實(shí)際控制中的作用不好說明，留在后面再說，但是到這里大家也就看出我為什么要使用標(biāo)準(zhǔn)的Kp Ti Td參數(shù)而不是Kp Ki Kd參數(shù)了，因?yàn)槭褂眠@種參數(shù)時(shí)Kp對(duì)開環(huán)系統(tǒng)的穩(wěn)定性（注意僅指開環(huán)系統(tǒng)）沒有影響，我們就可以降低系統(tǒng)對(duì)這個(gè)參數(shù)的敏感性而主要考慮另外兩個(gè)參數(shù)就好。大家在手調(diào)參數(shù)的看到的圖形和這個(gè)都應(yīng)該沒有多少區(qū)別

　　接下來我們看一下我們被控系統(tǒng)的數(shù)學(xué)模型：

　　被控系統(tǒng)的小范圍線性化模型

　　正如我前面所述，想要分析PID的控制性能必須得得到被控系統(tǒng)的線性近似模型（非線性系統(tǒng)下的分析工具沒個(gè)正經(jīng)能用的），這里大家可以通過動(dòng)力學(xué)建模得到系統(tǒng)的非線性模型（像幾乎所有的碩士博士論文那樣）再泰勒展開，但是這樣做往往得到的模型跟實(shí)際情況差異太大以至于沒有參考價(jià)值，這里我推薦使用系統(tǒng)辨識(shí)的方法來得到系統(tǒng)的線性模型，因?yàn)檫@么做如果能做到正確的辨識(shí)的話還能得到系統(tǒng)的誤差模型，于是現(xiàn)在在控制界很流行，只是實(shí)際用的時(shí)候就發(fā)現(xiàn)難度頗高，盡管有許多現(xiàn)成的工具但是依然特別難掌握，也難怪很多熱會(huì)把這個(gè)當(dāng)做是看家本領(lǐng)，作者在這方面也算是連皮毛都沒摸全，不敢亂講，這里就為了解釋PID方便直接把我的大四軸辨識(shí)出來的Pitch軸模型拿出來當(dāng)做例子來講了：

　　畫出來的系統(tǒng)階躍響應(yīng)是這個(gè)樣子的：

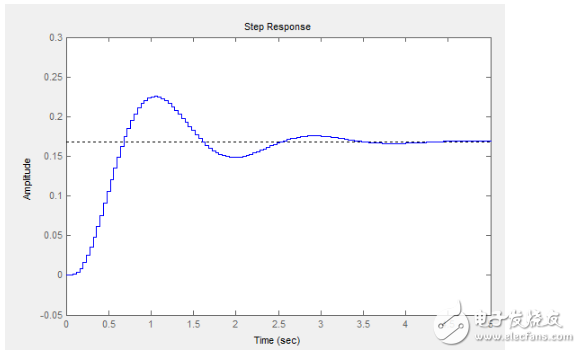
　　檢驗(yàn)系統(tǒng)建模的相似程度就靠這個(gè)了，給我的飛機(jī)一個(gè)階躍信號(hào)反映出來的情況和這個(gè)確實(shí)差不多。關(guān)鍵是下面，它的零極點(diǎn)分布情況：

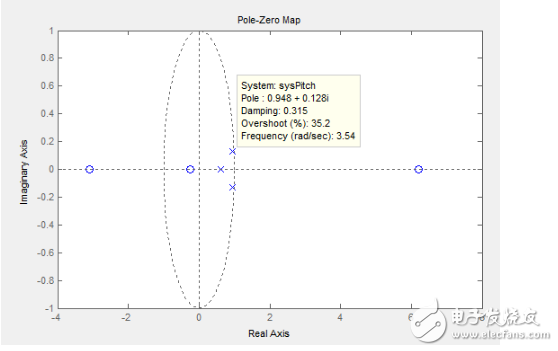
　　可以看到辨識(shí)出來的結(jié)果又兩個(gè)很靠近不穩(wěn)定邊界的主導(dǎo)極點(diǎn)（氣泡框那里）表現(xiàn)明顯的零點(diǎn)又和這幾個(gè)極點(diǎn)8桿子打不著，如果我們消滅那兩個(gè)主導(dǎo)極點(diǎn)，我們的四軸理論上就可以控制的非常完美了，眾所周知，主導(dǎo)極點(diǎn)越靠近0則系統(tǒng)穩(wěn)定性越好，那么按照極點(diǎn)配置的方法（當(dāng)然我這里指的還是開環(huán)的極點(diǎn)配置），那么我們接下來開始看用這種建模的方法怎么實(shí)現(xiàn)PID參數(shù)的配置：

　　用極點(diǎn)配置PID實(shí)現(xiàn)對(duì)系統(tǒng)的控制

　　那么按照上面的介紹我們來嘗試消除這兩個(gè)主導(dǎo)極點(diǎn)，前面說過，PID模型中兩個(gè)對(duì)稱零點(diǎn)的位置是可以任意調(diào)整的，不用計(jì)算，直接手試出如下的參數(shù)：

　　那么得到的開環(huán)零極點(diǎn)圖是這樣的：

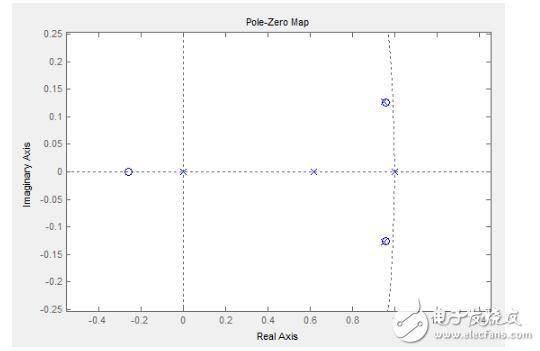
　　那么閉環(huán)響應(yīng)是這個(gè)樣子的：

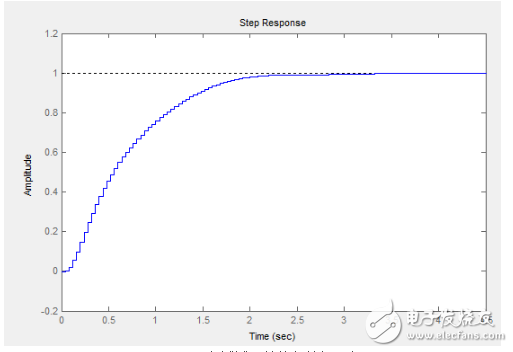
　　看著很漂亮啊，我們加大Kp到4試試，其他參數(shù)都不變

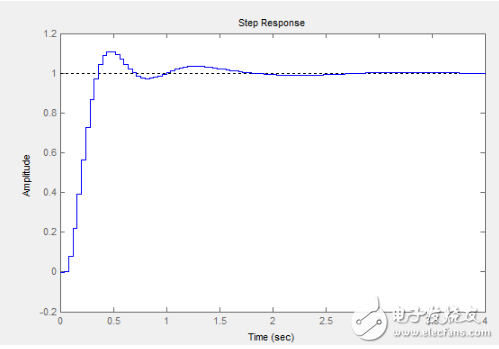
　　喲，完美嘛，0.5s即可到達(dá)穩(wěn)態(tài)，0穩(wěn)態(tài)誤差，超調(diào)量也不過10%而已，相當(dāng)?shù)睦硐耄覐倪@里可以看出使用Kp Ti Td參數(shù)的優(yōu)勢(shì)：隨意調(diào)整Kp，可以提高系統(tǒng)性能而且對(duì)閉環(huán)穩(wěn)定性幾乎沒有影響，甚至對(duì)開環(huán)系統(tǒng)的穩(wěn)定性完全沒有影響，我想，這也就是MWC飛控用Kp（角速度的）作為動(dòng)態(tài)參數(shù)的原因。那么好吧，令人沮喪的部分終于要來了，把這個(gè)參數(shù)燒到飛控里面，運(yùn)行，哇塞，不錯(cuò)哦，不動(dòng)搖桿它平衡的很好，那我們遙控下……我擦，越抖越大，控制不住了，翻了，打到人了，鮮血汩汩而出……………………