波特圖的定義
波特圖是線性非時變系統的傳遞函數對頻率的半對數坐標圖,其橫軸是頻率,縱軸以對數尺度(logscale)表示,利用波特圖可以看出系統的頻率響應。波特圖一般是由二張圖組合而成,一張幅頻圖表示頻率響應增益的分貝值對頻率的變化,另一張相頻圖則是頻率響應的相位對頻率的變化。
波特圖可以用電腦軟件(如MATLAB)或儀器繪制,也可以自行繪制。利用波特圖可以看出在不同頻率下,系統增益的大小及相位,也可以看出大小及相位隨頻率變化的趨勢。
波特圖的圖形和系統的增益,極點、零點的個數及位置有關,只要知道相關的資料,配合簡單的計算就可以畫出近似的波特圖,這是使用波特圖的好處。
波特圖(Bode Plots)
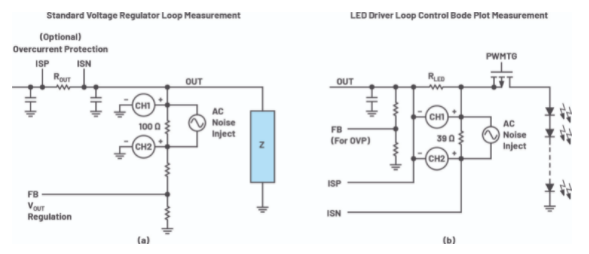
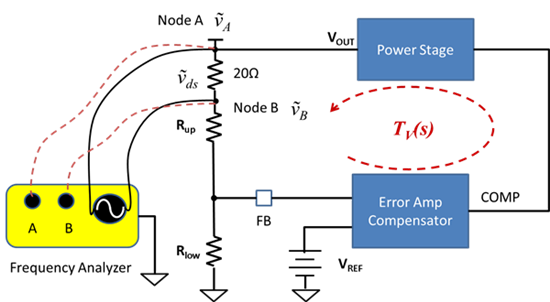
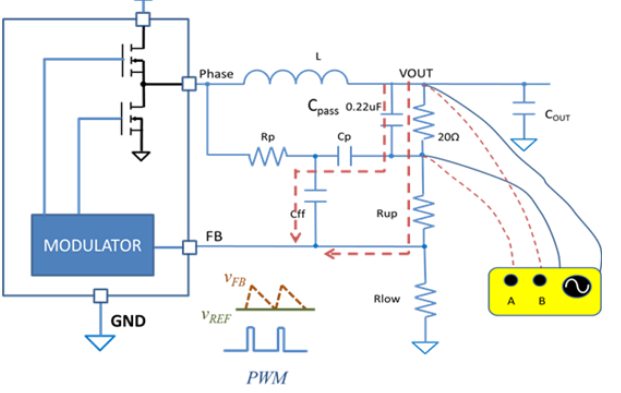
波特圖(Bode Plots)可用來確認回路的穩定性,回路的增益(Loop Gain,單位:dB)是頻率(Frequency)的函數(圖5:典型的波特圖)。 回路增益可以用網絡分析儀(Network Analyzer)測量。 網絡分析儀向反饋回路(Feedback Path)注入低電平的正弦波(Sine Wave),隨著直流電壓(DC)的不斷升高, 這些正弦波信號完成掃頻,直到增益下降到0dB。然后測量增益的響應(Gain Response)。

圖5
波特圖是很方便的工具,它包含判斷閉環系統(Closed-loop System)穩定性的所有必要信息。 包括下面幾個關鍵參數:環路增益(Loop Gain),相位裕度(Phase Margin)和零點(Zeros)、極點(Poles)。
波特圖分析
用包含三個極點和一個零點的波特圖(圖11:波特圖)來分析增益和相位裕度。

圖11
假設直流增益(DC gain)為80dB,第一個極點(pole)發生在100Hz處。在此頻率,增益曲線的斜度變為-20dB/十倍頻程。1kHz處的零點使斜度變為0dB/十倍頻程,到10kHz處斜度又變成-20dB/十倍頻程。在100kHz處的第三個也是最后一個極點將斜度最終變為-40dB/十倍頻程。
圖11中可看到單位增益點(Unity Gain Crossover,0dB)的交點頻率(Crossover Frequency)是1MHz。0dB頻率有時也稱為回路帶寬(Loop Bandwidth)。
相位偏移圖表示了零、極點的不同分布對反饋信號的影響。為了產生這個圖,就要根據分布的零點、極點計算相移的總和。在任意頻率(f)上的極點相移,可以通過下式計算獲得: 極點相移 = -arctan(f/fp) (6)
在任意頻率(f)上的零點相移,可以通過下式計算獲得: 零點相移 = -arctan(f/fz) (7)
此回路穩定嗎?為了回答這個問題,我們根本無需復雜的計算,只需要知道0dB時的相移(此例中是1MHz)。
前兩個極點和第一個零點分布使相位從-180°變到+90°,最終導致網絡相位轉變到-90°。最后一個極點在十倍頻程中出現了0dB點。代入零點相移公式,可以計算出該極點產生了-84°的相移(在1MHz時)。加上原來的-90°相移,全部的相移是-174°(也就是說相位裕度是6°)。由此得出結論,該回路不能保持穩定,可能會引起振蕩。
波特圖應用
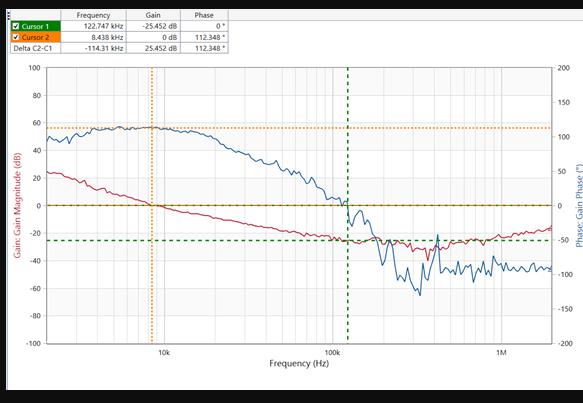
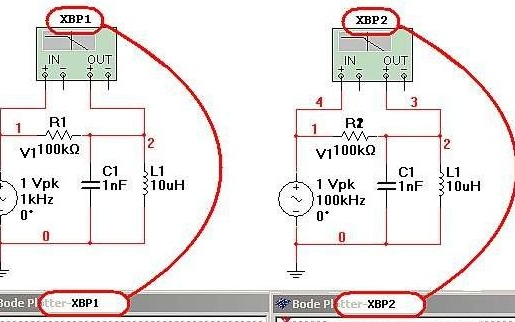
現在以一簡單的低通濾波器來窺探下波特圖的魅力。
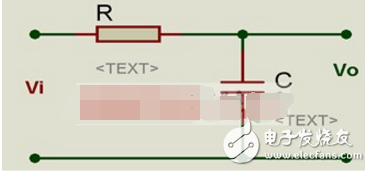
傳遞函數

我們將該點叫做頻率轉折點,在頻率較低的范圍內,增益大約為1,在頻率較高的范圍內,系統增益以-20dB/10倍頻的速度下降。在濾波器設計中,也就是我們常聽到的3dB帶寬的截止頻率。低通濾波器的波特圖頻率響應部分如下所示:
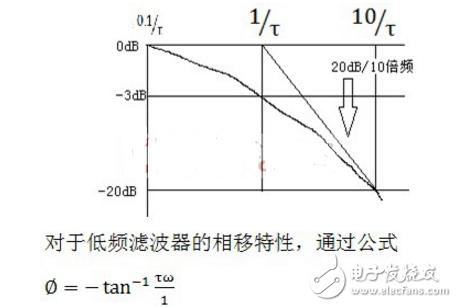
由于正切函數是非線性的,描述其特性比較難搞,其實我們可以依據我們擁有的基礎數學知識來近似描述該函數:

位為0°、45°和90°。在波特圖的相頻圖中畫出相應曲線,如下圖所示:
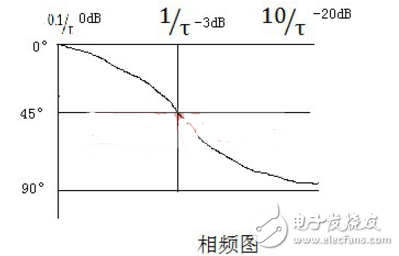
以上以一簡單的一階低通濾波器作為例子進行系統的波特圖分析和畫制,在實際的工程中,常常會因為采用多個電容和電阻構成了更加負責的系統,其實原理分析都是如此,只不過在分析過程中,找出關鍵位置的頻率點,就能掌握系統傳遞函數的綱要,達到高屋建瓴的效果。
在多極點和零點傳遞函數中,使分母為零的頻率點叫極點,使分子頻率為零的頻率點叫零點,極點可以使增益曲線下降,零點使增益曲線上升。在多極點和零點的系統中,只要找到各個極點和零點,找出其特性,將各個增益曲線疊加即可實現系統的極零分析,這個定理可以幫助大家在畫多極點和零點的傳遞函數有個直觀的印象。
 電子發燒友App
電子發燒友App










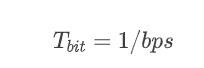
















評論