浮點算法不遵循整數算法規則,但利用 FPGA 或者基于 FPGA 的嵌入式處理器不難設計出精確的浮點系統。
工程人員一看到浮點運算就會頭疼,因為浮點運算用軟件實現速度慢,用硬件實現則占用資源多。理解和領會浮點數的最佳方法是將它們視為實數的近似值。實際上這也是開發浮點表達式的目的。正如老話所說,真實的世界是模擬的,有許多電子系統在與真實世界的信號打交道。因此,對于設計這些系統的工程師來說,有必要理解浮點表達式以及浮點計算的優勢和局限性。這將有助于我們設計可靠性更高、容錯性更好的系統。
首先深入了解一下浮點運算。通過一些示例計算就可以看到浮點運算不如整數運算直接,工程師在設計使用浮點數據的系統時必須考慮這一點。這里有個重要的技巧:用對數來運算極小的浮點數據。我們的目的是熟悉一些數值運算的特點,把重點放在設計問題上。本文結尾列出的參考文獻中有更加深入的介紹。
就設計實現而言, 設計人員可以使用賽靈思LogiCORE? IP Floating-Point Operator 生成和實例化RTL 設計中的浮點運算符。如果采用 FPGA 中的嵌入式處理器構建浮點軟件系統,則可以使用 Virtex-5 FXT 中面向PowerPC 440 嵌入式處理器的 LogicCORE IP Virtex?-5輔助處理器單元 (APU) 浮點單元 (FPU)。
浮點運算 101
IEEE 754-2008 是現行的浮點運算 IEEE 標準。(1)它取代了該標準的 IEEE 754-1985 和 IEEE 754-1987 版本。該標準中的浮點數據表達規則如下:
? 要求零帶符號:+0,-0
? 非零浮點數可表達為 (-1)^s x b^e x m,這里:s 為 +1 或者 -1,用于表明該數為正數還是負數,b是底數(2 或者 10),e 是指數,m 則是以 d0.d1d2—dp-1 形式表達的數,這里 di 對以 2 為底數的情況可以是 0 或者 1,對以 10 為底數的情況可以是0 和 9 之間的任意值。請注意小數點應緊跟 d0。
? 分正負的極限:+∞,-∞。
? 非數值,有兩種形式:qNaN(靜態)和 sNaN(信號)。
表達式 d0.d1d2—dp-1 指“有效值”,e 為“指數”。有效值總共有 p 位數,p 即為表達式的精度。IEEE754-2008 定義了五種基本的表達式格式,三種用于 2 為底數的情況,兩種用于 10 為底數的情況。標準中還提供更多的衍生格式。IEEE 754-1985 中規定的單精度浮點數和雙精度浮點數分別稱為 binary32 和 binary64。對每種格式都規定有最小的指數 emin 和最大的指數 emax。
可以用浮點數格式表達的有限值的范圍取決于底數(b)、精度 (p) 和 emax。該標準一般將 emin 定義為1-emax:
? m 是 0 到 b^p-1 內的整數
例如,在 p=10 和 b=2 的情況下,m 就介于 0 到1023 之間。
? 對給定的數,e 必須滿足下式
1-emax<=e+p-1<=emax
例如,如果 p=24,emax=+127,則 e 的取值范圍是-126 到 104。
這里需要清楚一點,即浮點表達式往往不是唯一的。
例如,0.02x10^1 和 2.00x10^(-1) 都代表相同的實數,即0.2。如果第一位數 d0 為 0,則稱該數值被“標準化”。同時,對某個實數來說,可能不存在浮點表達式。例如,0.1 在十進制中是一個確定的值,但它的二進制表達式是一個小數點后 0011 的無窮循環。因此,0.1 無法用浮點格式確定地表達。表 1 給出了 IEEE 754-2008 規定的五種基本格式。

浮點計算的誤差
因為要用固定位數來表達無窮數量的實數,因此在浮點計算中四舍五入是必不可少的。這就會不可避免地帶來舍入誤差,故需要有一種方法來衡量結果與采用無窮精度計算時的差距。我們來觀察一下 b=10 和 p=4 的浮點格式。用這種格式,.0123456 可以表達成 1.234x10^(-2)。很明顯這種表達方式在最后位置單位 (ulps) 發生了 .56 的差異。又如,如果浮點計算的結果是 4.567x10^(-2),而采用無窮精度計算的結果是 4.567895,則最后差 .895 最后位置單位。
“最后位置單位”(ulps) 是規定這種計算誤差的一種方法。相對誤差是另一種用來衡量浮點數近似實數誤差的方法。相對誤差被定義為實數與浮點數之差除以實數的商。比如,將 4.567895 用浮點數表達為 4.567x10^(-2) 時的相對誤差為 .000895/4.567895≈.00019。根據標準的要求,每個浮點數的正確計算結果的誤差應不大于 0.5ulps。
浮點系統設計
在為數值應用開發設計的時候,很重要的一環是考慮輸入的數據或者常數是否可以為實數。如果可以為實數,則在完成設計之前需要注意一些問題。需要檢驗來自數據集的數值在浮點表達式中是否很接近,有沒有出現過大或者過小的情況。下面以二次方程求根為例。二次方程的根α 和 β 分別表達為下面兩個等式:
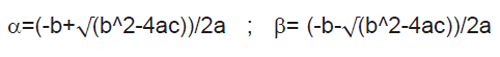
很明顯,如果 b^2 和 4ac 是浮點數,就會遇到舍入誤差問題。如果 b^2 遠大于 4ac,則 √(b^2 ) =|b|。如果b>0,β 將有解,但 α 的解將為 0,因為其分子中的各項相互抵消。另一方面,如果 b < 0,則 β 的解為 0,α 將有解。這是一種錯誤的設計,因為在浮點計算的作用下,根的值為 0,如果用于后續的設計,將很容易導致錯誤的輸出。
防止這種錯誤抵消的方法之一是將 α 和 β 的分子和分母同時乘以 -b-√(b^2-4ac),這樣得到:
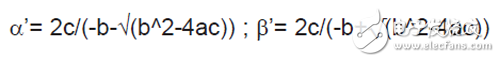
現在,在 b>0 的情況下,應使用 α’ 和 β 求出兩個根的值。在 b<0 的情況下,應使用 α 和 β’ 求出兩個根的值。在設計中很難察覺到這樣的誤差,原因在于對于整數數據集來說,常規公式會得出正確的結果,但在使用浮點數據的時候,常規公式會讓設計返回錯誤的結果。
另一個有趣的實例是計算三角形面積。根據 Heron 公式,在已知三角形邊長的情況下,三角形的面積 A 可以用下面的公式求出:
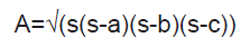
這里 a,b 和 c 是三角形的邊長,s= (a+b+c)/2。
對一個一邊的長度約等于另外兩邊長度之和的平三角形而言,有 a≈b+c,隨即有 s≈a。由于兩個相鄰的數值會在 (s-a) 中相減,所以 (s-a) 可能會等于 0。或者,如果 s或者 a 出現舍入誤差,就會導致顯著的 ulps 誤差。因此,最好根據數學家和計算機科學家 William Kahan (2)在 1986 年率先提出的建議,將此公式改寫為下列格式:
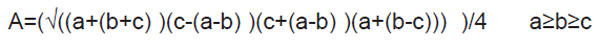
我們看看分別用 Heron 的公式和 Kahan 的公式對相同的數值進行計算的結果如何。假定 a=11.0,b=9.0,c=2.04,則正確的 s 值為 11.02,正確的 A 值為1.9994918。但是,在采用 Heron 公式的情況下,計算得出的 s 值為 11.05,只有 3ulps 的誤差,A 的值為3.1945189,出現巨大的 ulps 誤差。在采用 Kahan 的公式的情況下,得出的 A 值為 1.9994918,小數點后七位完全與正確的結果吻合。
處理極小和極大的浮點數
極小的浮點數在相乘后會得出更小的結果。對設計人員來說,這可能會導致系統的下溢問題,最終的結果可能出錯。這個問題在概率處理領域中尤為突出,比如計算語言學和機器學習。任何事件的概率一般都在 0 和 1 之間。能夠得到完美整數結果的公式在處理非常小的概率時往往會導致下溢問題。避免下溢的方法之一是采用指數和對數。
在對很小的浮點數做相乘運算時,采用下面的公式非常有效:

這里指數和對數的底數必須相同。不過需要注意的是,如果a 和 b 都是概率,值都在 0和 1 之間,那么它們的對數會在-∞ 和 0 之間。如果只希望處理正概率,則將概率的對數乘以 -1,就可以正確地解讀結果。采用對數值的另一項優勢在于速度,因為相加比相乘的操作速度更快。
工程人員往往會遇到需要對非常大的連續數進行相乘的情況,比如:
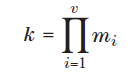
K 的值在某些情況下非常容易溢出。處理這種情況的方法之一是用下式計算 k:
當然,這樣計算相對較為復雜一點,但如果想要保證設計在計算這種極端狀況時不會出錯,這點代價還是值得的。
一些常見的浮點微妙之處
浮點算術并不嚴格遵循整數的數學規律。加法和乘法結合律對浮點數無效,減法和除法也是如此。造成這種情況的原因有兩個。首先在順序變動時會出現下溢或者上溢,其次是舍入誤差問題。請看下面關于浮點數 a,b 和 c的幾個例子。
右邊的表達式在 a 和 b 相乘時可能出現上溢或者下溢。另外,由于 a 和 b 的乘積先計算,它的舍入誤差與左邊 b 和c 乘積的舍入誤差不同,結果導致兩個表達式得出的結果不同。
左邊的 (b-c) 表達式中,如果兩個數的浮點表示足夠接近,會使該項結果為 0。在這種情況下 a=c。(b-c) 的舍入誤差會導致結果與 b 不同。
由于舍入誤差,表達式 (1.0+c) 的結果會導致值發生改變,最終與第一個表達式的結果不同。
同理,c/10.0 的舍入誤差與 cx0.1 的不同,導致 b 的值不同。另外,數值 10.0 可以用 2 為底數表達為確切的表達式,但數值 0.1 用 2 為底數不能表達為確切的表達式。數值0.1 在表達為二進制表達式時,會出現 0011 的無窮循環。這種不能用特定的底數進行有限表達的數被稱為該底數的非確定數,而能夠進行有限表達的,則被稱為確定數。
假定 c 可以一直被表達為確定數,如果 c 在一種情況下與確定數相除,在另一種情況下與非確定數相乘,則得到的結果是不一樣的。而且由于 c 本身也可以是確定數或不確定數,取決于之前的計算方法,所以兩個表達式之間的等價性無法成立。
這個等式在 x 為 0、無窮或者非數值的情況下是不成立的。在執行無效數學運算的情況下會出現 NaN,比如開負數的平方根或者用 0 除以 0。在出現 NaN 的情況下,程序員負責決定下一步怎么做。應注意根據 IEEE 754-2008 的規定,NaN 可以用指數 emax+1 和非零有效數表達為浮點數。因為有效數中可以放入由系統決定的信息,故結果將是一系列NaN 而非唯一的 NaN。因此在處理浮點代碼時,請勿用 1.0替換 x/x,除非能夠確認 x 不是零、無窮或者 NaN。
在 x 為無窮或者 NaN 的情況下該等式不成立。因此在不能確定 x 取值的情況下請勿用 0.0 替換 x-x。工程人員往往在編譯器中采用這種替換技巧作為優化策略。但是正如所看到的,這樣的優化可能導致錯誤的結果。
上面的等式在 x 為 -0 的時候不成立(注意可以有 +0 和-0)。這是因為根據 IEEE 754-2008 規定的默認舍入規則,(-0) + (+0) =+0,經舍入后為偶數。
IEEE 標準定義 +0 和 -0 的目的是為了得出答案的符號。比如 4 x (+0) =+0,(+0)/(-4)=-0。為比較目的,可以令+0=-0,這樣像 if (x=0) 這樣的聲明就不用關心 +0 和 -0 之間的差異了。
更深入的理解
除了 Kahan 的著作,想要更加深入地領會使用浮點數據的各種微妙之處,工程人員還可以閱讀 Goldberg 博士的《What Every Computer Scientist Should Know AboutFloating-Point Arithmetic》A 版(加利福尼亞州 Mountain View,1992 年 6 月)。另外有大量優秀參考文件對 IEEE 754-2008 標準以及其他影響浮點設計的標準(比如 ISO/ IEC 9899:201x)進行了詳細解讀。(3)
像航空電子和安全嵌入式系統這樣的電子行業領域要求開發高度精確且無誤的硬件和軟件。由于部分硬件需要處理大量的浮點數據,因此設計人員有必要掌握浮點算術與整數算術之間的差異。
 電子發燒友App
電子發燒友App





















評論