1?? 引言
隨著毫米波技術的發展, 對開關電源的性能提出了更高的要求。除了要求電源系統具有輸出電壓精度高、輸出紋波低、輸出過沖小的特點外, 還要求電源具有快速的動態響應。動態響應指標對應的是電源脈沖負載問題。由于開關電源具有有限的響應速度, 對于突變的負載, 電源系統不能及時響應輸出的變化, 造成輸出電壓的跌落。在用于脈沖負載的電源系統中, 維持輸出電壓的穩定是相當困難的。
本文通過對脈沖負載的機理進行理論分析, 對傳統的開關電源拓撲結構進行分析、仿真、計算, 找出不同結構之間實現脈沖負載的差異; 得到能夠實現中小功率脈沖負載的拓撲結構。通過設計實例,證明了該結構的優點。
2?? 脈沖負載原理與仿真
2. 1?? 脈沖負載原理
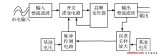
基于脈沖負載的開關電源結構如圖1 所示。整個結構由輸入電壓VIN 、功率變換PWM、輸出濾波電感L 和輸出濾波電容C 、脈沖開關G、負載RLOAD組成。濾波電容包含等效電阻Cesr 和等效電感Cesl 。
?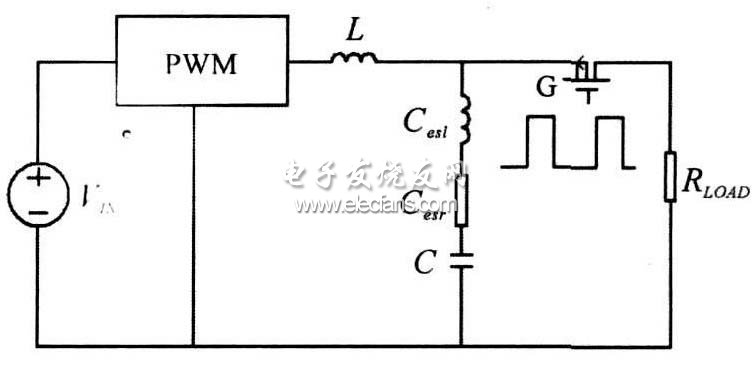
圖1?? 基于脈沖負載的開關電源
電路基本原理是: PWM 控制單元將輸入電壓VIN 轉換為固定的輸出VOUT , 輸出連接一個PMOS開關管, 通過脈沖信號, 將功率傳輸到負載; 此時, 流過負載RLOAD 的電流是脈動的。
在控制脈沖到來時, 功率開關管G 導通, 負載電流開始線性增加, 如圖2 所示。輸出電流從0 A開始, 在T r 時間內, 上升到固定輸出電流I out 。通常, T r 為納秒級。開關電源的開關頻率通常為幾百kHz。在這樣短的時間內, 由于開關電源的控制回路存在延遲, 來不及反映輸出電壓的變化情況, 不能將輸入電源的能量傳遞到輸出電容, 以便補充負載從電容上消耗的能量。換句話說, 在T r 時間內, 負載所消耗的能量只能從電容上拉取。
?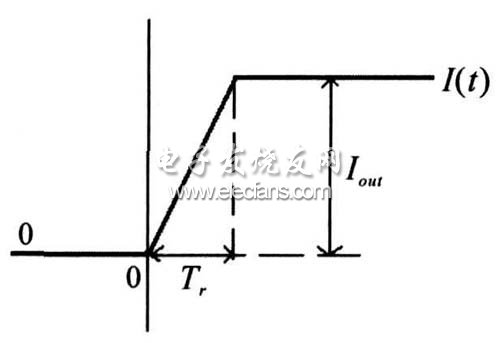
圖2? 負載電流上升時序
由于電容在高頻下等效為電容和電阻、電感的串聯模型, 所以, 在T r 時間段內, 負載電容上的電壓跌落應該是電容和等效電阻、等效電感三者共同作用的結果。由電荷相等公式( 1) , 可得電容產生的跌落電壓( ( 2) 式) :
?
式中,
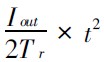
表示在電流上升過程中三角形的面積。
電阻產生的跌落可由( 3) 式得到:
?
電感產生的跌落可以由( 4) 式得到:
?
在Tr 時間段內, 由負載突變造成的輸出電壓跌落為:
?
在負載電流達到最大值后, 電容上的電壓繼續跌落, 直到反饋系統開始工作, 電感的平均電流等于負載電流時, 電容上面的電壓才開始回升。反饋系統開始工作, 取決于反饋系統的響應速度, 也就是取決于整個電源環路的帶寬。假設整個環路的的交叉頻率為f 。, 輸出電壓的跌落可以通過交叉頻率f 處的輸出濾波電容的容抗計算 。輸出電容在交叉頻率處的容抗為:
?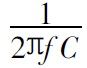
故由反饋環路引起的電壓跌落可以由( 6) 式得到:
?
2. 2?? 脈沖負載仿真
根據脈沖負載原理, 構建一個非隔離Buck 控制器進行仿真。開關頻率為400 kHz, 濾波電容的等效電阻為50 mΩ ,等效電感為10 nH, 電容容量為330μ F,整個回路的交越頻率為25 kHz。仿真結果如圖3所示。脈沖負載幅度為3 A, 上升時間50 ns。
?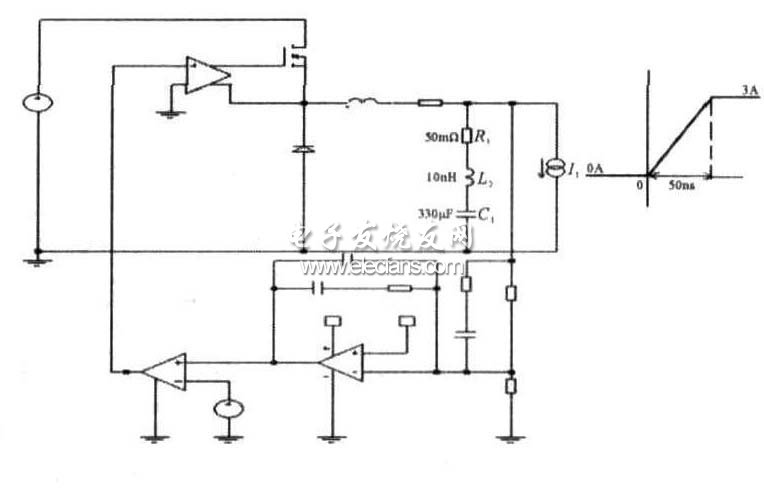
圖3?? 脈沖負載原理仿真
電路仿真結果如圖4 所示。輸出電壓波形在突然增加負載時開始跌落, 由于整個PWM 的反饋系統還沒有起作用, 電容的電壓被拉低, 形成一個凹陷。隨著PWM 開始檢測到輸出電壓的降低, 開始從輸入端傳遞能量到濾波電容上, 電容的電壓開始回升, 直到回到穩定值。電壓從跌落到恢復到穩定值的過程中, 沒有出現振蕩, 表明在此參數條件下,整個電源環路具有合適的增益余量和相位余量。
?
圖4?? 脈沖負載輸出電壓
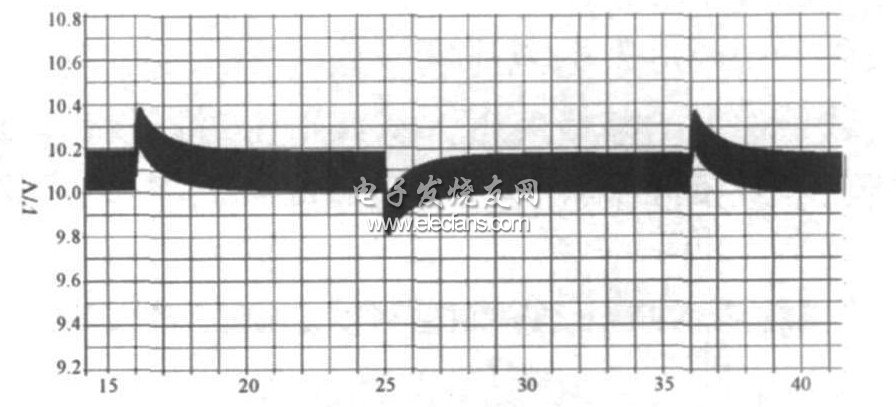
局部放大波形如圖5 所示。圖6 是圖5 中B 處的放大時序, 此處的凹陷主要由電容上等效電感和等效電阻的影響造成。從仿真圖上可以看出, 等效電感引起的跌落為601 mV, 與用( 4) 式計算的結果( 600 mV) 相當。當負載電流達到最大值后, 電壓開始回升600 mV。等效電感造成的電壓跌落消失。等效電阻產生的最大跌落為Iout×Cesr = 150 mV, 與仿真結果145 mV 一致。
?
圖5 圖4中A處的放大波形
從圖5 可以看出, 當負載電流達到最大值后, 等效電感產生的電壓跌落消失, 等效電阻產生的電壓跌落達到最大值150 mV。隨后, 電容電壓繼續跌落, 待反饋回路起作用后, 電感的平均電流等于負載電流時, 輸出電壓開始回升, 最終回到穩定的狀態。
從圖5 可以看出, 反饋環路響應速度的快慢影響著輸出電壓的跌落幅度。
3?? 幾種控制方式的比較
3. 1?? 影響脈沖負載的主要因素
由脈沖負載的基本原理可以得到, 影響電壓跌落的因素有輸出電容的等效電阻、等效電感和輸出電容的容量以及反饋環路的響應速度。負載電流變換越快, 等效電感導致的電壓跌落幅度越大。在實際電路中, 輸出電容的等效電阻、等效電感可以通過選取合適的電容及合理的版圖布局進行改善。從圖6 可以看出, 影響電壓跌落的幅度歸咎到反饋環路的響應速度, 即取決于反饋環路的帶寬。
?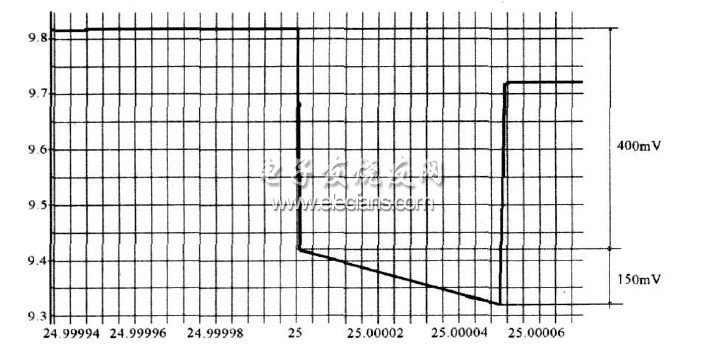
圖6 圖5中B處的放大波形
在非隔離的電源中, 線性穩壓器可以實現很寬的帶寬, 通常可大于500 kHz。因此, 線性穩壓器能顯著減小負載突變時輸出電壓的跌落幅度, 也可以減少輸出濾波電容, 但是, 線性非隔離變換器存在效率低的缺點。在隔離的變化器中, 由于存在反饋環路的延遲, 尤其是采用光耦隔離的電源, 光耦的帶寬通常小于10 kHz, 整個電源系統必須降低帶寬, 才能實現環路的穩定。帶寬的減小導致整個系統具有很大的反饋延遲, 在負載變化時, 加劇了輸出電壓的跌落幅度。在反饋慢的系統中, 除了增加輸出儲能電容外, 沒有其他更好的辦法。
?
3. 2?? 非隔離變換器中脈沖負載的研究
相對于隔離變換器, 非隔離變換器由于減少了隔離變壓器, 體積更小; 同樣, 由于沒有光耦等隔離反饋, 容易提升整個反饋環路的帶寬, 使之更適合于脈沖負載。在中小功率電源中, 主要是升壓和降壓結構。
3. 2. 1?? 升壓結構脈沖負載分析
圖7 是典型的升壓拓撲結構, 由脈寬控制器、開關管Q1、電感L 1、整流二極管D1, 濾波電容C1 和反饋取樣電阻R1、R2 組成。
?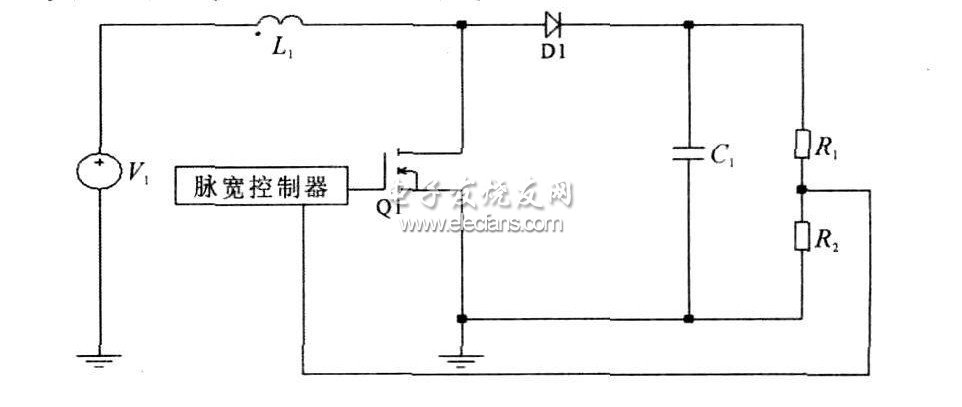
圖7?? 典型升壓電路結構
分析升壓電路的工作原理, 通過電感的伏秒平衡, 可以得出輸出電壓和輸入電壓之間的關系為Vo= Vin / ( 1- D) 。升壓結構只適用于輸出電壓比輸入電壓高的場合。在電感電流連續模式下, 通過PWM 開關模塊分析, 可以得出電壓控制連續模式升壓電路的小信號傳輸:
?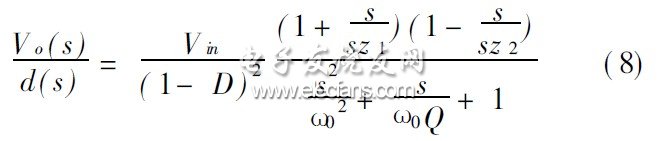
從( 8) 式可以看出, 整個回路存在一個右平面零點。右半平面零點與電路中經常用于提升相位的左半平面零點有著本質的不同: 左半平面零點能夠提升相位, 使系統更加穩定; 而右半平面零點則是隨著頻率的增加, 相位進一步降低, 引起系統的不穩定。
由于存在右半平面零點, 在電流連續模式的升壓結構中, 只有降低環路的帶寬來避開右半平面零點。
右半平面零點存在的位置sz 2 = 1/ (RES×C) 。根據脈沖負載的原理, 當電源工作在脈沖負載時, 除了要提升帶寬外, 還要加大輸出電容的容量。加大輸出電容的容量, 必然導致右半平面零點的減小, 這樣就需要再次減小電路的帶寬, 最終導致在動態負載時輸出電壓跌落更多。升壓電路有電壓控制和電流控制方式。兩種控制方式都不能消除連續模式下的右半平面零點問題, 這就限制了升壓結構在脈沖電源中的應用。
3. 2. 2?? 降壓結構脈沖負載分析
圖8 是典型的降壓電路結構, 整個電路由開關管、整流二極管、電感、濾波電容以及反饋驅動電路組成。
?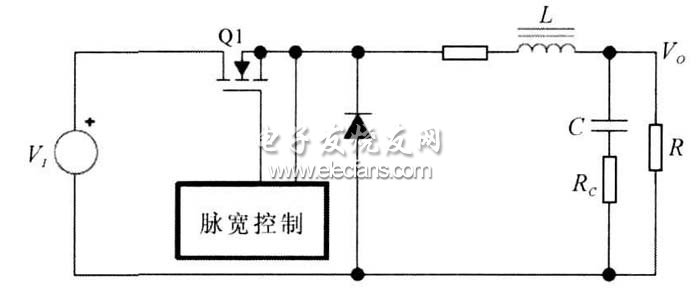
圖8?? 基本的降壓電路結構
通過電感的伏秒平衡, 可以得到輸入輸出之間的傳遞函數: V o= V in×D(D 為開關的占空比) 。降壓電路只能用于輸出電壓比輸入電壓低的場合。通過PWM 模型分析,得到電壓連續模式降壓電路的小信號傳輸函數:
?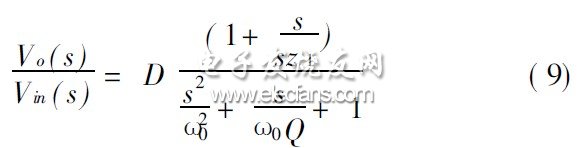
從( 9)式可以看出, 相對于升壓電路, 工作于電感電流模式的降壓電路沒有右半平面零點。因此, 降壓電路控制器就可以在很大范圍內提升整個環路的帶寬, 減小環路的響應時間, 降低輸出電壓的跌落幅度。
同樣, 降壓控制器有電壓控制模式、電流控制模式、遲滯控制模式、恒定導通時間模式。遲滯控制模式和恒定導通模式通過對負載電流的取樣, 可以在很短的時間內實現環路響應。但是, 恒定導通模式和遲滯控制模式的開關頻率是變化的, 造成變化的EMI 干擾, 不利于電磁兼容設計。相對于電壓控制模式, 電流控制模式更能夠實現環路的補償, 有利于實現環路的寬帶寬。因此, 降壓型變換器有利于實現脈沖負載電源。
3. 3?? 隔離變換器的脈沖負載分析
隔離變換器主要有反激變換器、正激變換器、橋式變換器。反激變換器和正激變換器都可以用在中小功率的場合, 橋式變換器主要用在大功率場合。
因此, 在脈沖電源中, 適合中小功率脈沖負載的電源結構是反激變換器和正激變換器。
?
3. 3. 1?? 反激變換器脈沖負載分析
圖9 是典型的反激變換器結構。相對于升壓變換器, 反激變換器增加了一個變壓器, 實現了輸入輸出的隔離。
?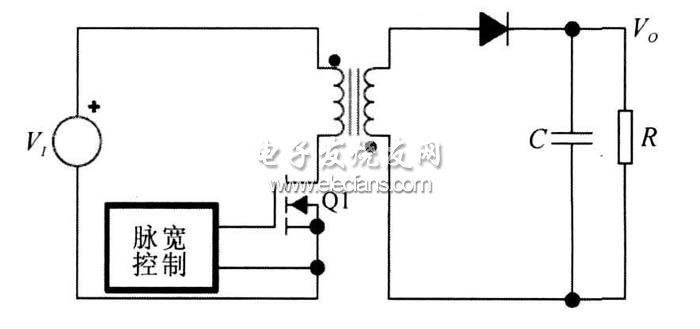
圖9?? 基本的反激變換器結構
通過對變壓器進行伏秒平衡分析, 得到電流連續模式下反激變換器的傳輸關系:
?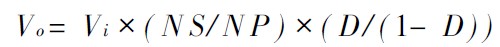
相對于升壓變換器, 反激變換器只增加一個變壓器。從本質上講, 其小信號傳輸關系是在升壓變換器的小信號關系上增加變壓器匝比。因此, 電壓連續模式反激變換器的小信號傳輸關系為:
?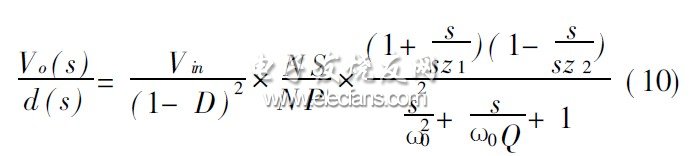
從( 10) 式可以看出, 工作在連續模式下的反激變換器同樣存在右半平面零點sz 2。與升壓變換器一樣, 反激變換器也不能實現寬的環路帶寬, 因此,反激變換器也不適合用于脈沖負載電源。
3. 3. 2?? 正激變換器的脈沖負載分析
典型的正激變化器結構如圖10 所示。正激變換器的工作原理與降壓型變換器相同, 增加了一個用于輸入輸出隔離的變壓器。
?
圖10? 正激變換器結構
工作于電壓模式連續的正激變換器小信號傳遞函數為:
?
相對于降壓變換器控制器的傳遞函數, ( 11) 式只是增加了變壓器的匝比。因此, 正激變換器沒有右半平面零點, 能夠實現寬的帶寬, 減小因脈沖負載造成的跌落。相對于降壓變換器控制器的多種控制方式, 正激變換器主要有電壓控制和電流控制方式。
由于電流控制方式更容易補償環路, 因此, 在正激變換器中, 主要采用電流控制模式。
負載電流是從0 到滿載, 正激變換器往往從空載到滿載變換。由于需要跨越輸出電感電流從非連續到連續模式, 增加了環路的響應時間。因此, 最好讓正激變換器工作在連續模式, 而不管負載電流的變化。一種方法是在輸出添加假負載, 但是會造成電路的效率下降, 另一種特別有效的方式是采用同步整流方式。同步整流的好處是可以提高效率, 但它更突出的特點是能夠使電路工作在連續模式。
?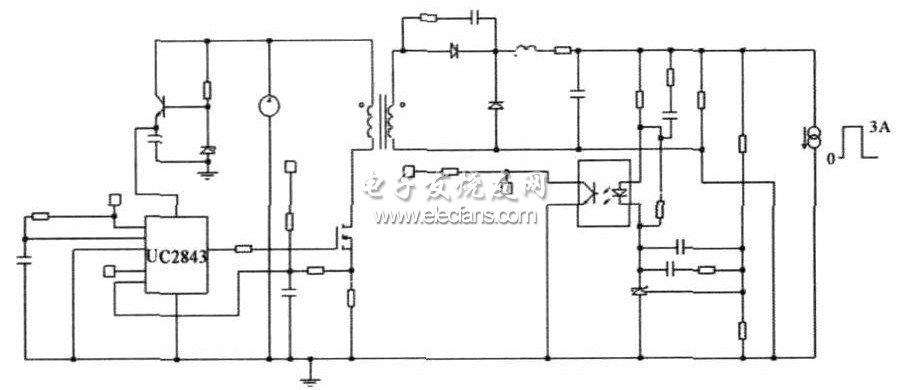
圖11 采用二極管整流方式的正激變換器
?
由于采用二極管整流方式, 當工作在輕載時, 整個電路工作在電流斷續模式; 當突然加負載時, 電路過渡到連續模式。其脈沖負載的仿真波形如圖12 所示。
?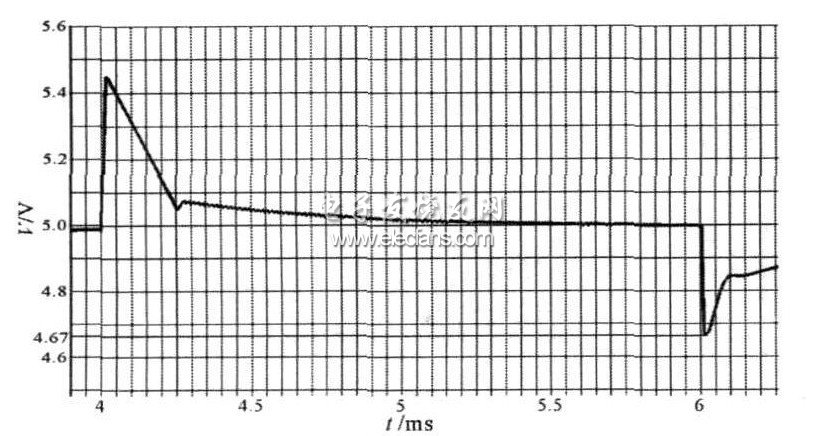
圖12 采用二極管整流方式的脈沖負載的仿真波形
從圖12 可以看出, 由于存在模式的突變, 在突然添加負載時候, 輸出電壓跌落為0. 5 V.
圖13 是采用同步整流方式的正激變換器, 整個電路工作在電流連續模式; 圖14 是采用同步整流方式的正激變換器仿真波形。從圖中可以看出, 采用同步整流方式, 在脈沖負載條件下, 輸出電壓的波動在0. 2 V 以內。
?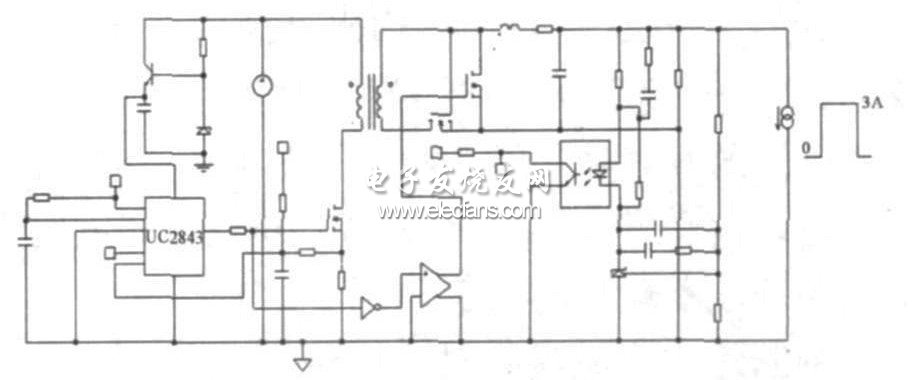
圖13 采用同步整流方式的正激變換器
?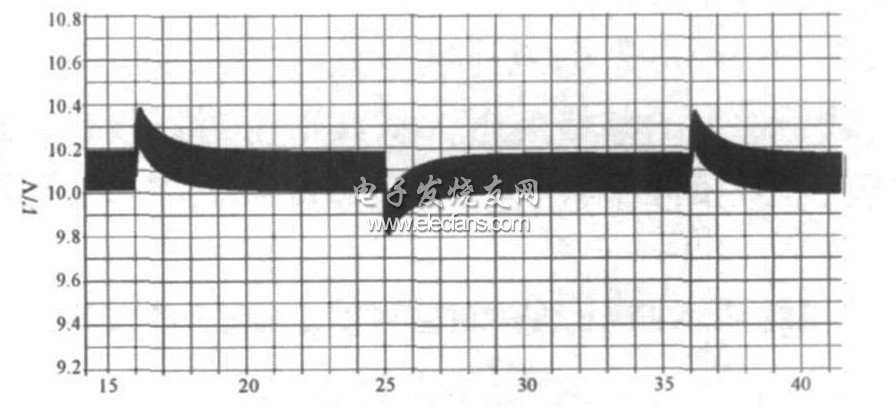
圖14 同步整流方式的正激變換器仿真波形
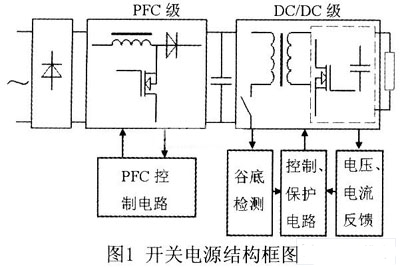
4?? 實驗驗證
采用正激結構加同步整流方式, 設計了一個隔離的脈沖負載電源。電路輸入電壓為17~ 36 V, 輸出為6 V/ 3 A , 開關頻率為200 kHz, 輸出濾波電容為200? F, 要求在3 A 負載時輸出電壓跌落小于0. 2 V。圖15 為本文設計的線路圖, 控制器采用電流型脈寬控制器LM5026, 其中整流MOS 管Q1 采用自驅方式, 同步整流管Q 2 采用變壓器隔離驅動方式。圖16 為實驗驗證電路的版圖。
?
圖15 本文設計的脈沖負載電源線路
?
圖16 本文設計的脈沖負載電源版圖
?
由于采用同步整流方式, 輸出濾波電感的電流是連續的。當負載很輕時, 輸出電感的電流方向會反向, 并通過續流MOS 管Q2 到地繼續流動。電流連續模式的好處就是整個控制器在脈沖負載條件下工作時, 不會出現從非連續模式到連續模式的突變,更利于變壓器環路的穩定。
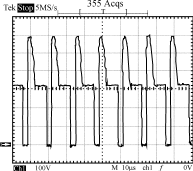
判斷輸出電感是否進入連續模式, 可以通過測試輸入PWM 控制器的輸出脈沖占空比來測定, 或者是初級開關管漏極波形來判斷。如果變換器從空載到滿載條件下占空比不變, 則表明變換器在空載條件下已經進入電流連續模式。圖17 是變換器在空載條件下的漏極波形。從波形上可以看出, 變換器在空載條件下開關頻率為200 kHz, 漏極波形占空比為59. 18%。
?
圖17? 空載時的漏極波形
圖18 是變換器帶載3 A 時的漏極波形。從波形上可以看出, 在帶載條件下, 漏極波形的占空比為59. 78%, 與空載基本一致, 表明電路在空載時已經進入連續模式。由于電源環路的截止頻率必須小于開關頻率的1/ 5, 為了更好地抑制紋波, 通過對環路補償進行設置, 將截止頻率設定在開關頻率的1/ 10處, 即20 kHz。由( 6) 式可以算出, 在3 A 負載下,輸出電壓的跌落為0. 119 V。圖19 是實際測試脈沖負載時的輸出電壓波形。從圖中可以看出, 輸出電壓的跌落為0. 1 V, 與計算值相當, 證明正激變換器加同步整流適合于脈沖負載電源。
?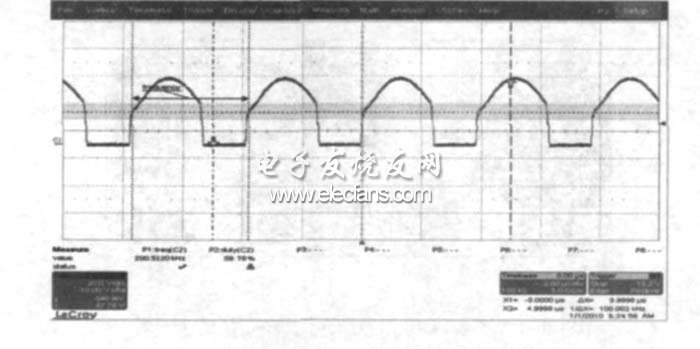
圖18? 滿載時的漏極波形
?
圖19? 輸出電壓波形
5?? 結論
本文通過對脈沖負載的機理分析、計算、仿真,驗證了在小功率非隔離變換器中升壓結構不適合脈沖負載結構, 降壓變換器加同步整流是最適合脈沖負載的拓撲結構。降壓變換器控制器可實現很寬的帶寬; 引入同步整流, 可以使整個電路工作在電流連續模式。在小功率隔離變換器中, 反激變換器同樣因為右半平面零點的影響而不適合用于脈沖負載。
正激變換器加同步整流可以顯著減小脈沖負載輸出電壓的跌落; 同時, 采用電流模式, 可以很好地對環路進行補償, 提升環路的帶寬。實驗電路驗證了同步整流正激變換器在脈沖負載中的可行性。
 電子發燒友App
電子發燒友App























評論