0 引言

　　BOC調制信號的頻譜分裂在中心頻點的兩側，有利于避開與中心頻點信號頻譜的相互重疊，從而減小信號間的相互干擾，以實現頻段共用。此外，BOC調制信號比BPSK調制信號的相關函數主瓣更窄，它具有更高的碼跟蹤精度和更強的抗多徑干擾能力。由于BOC調制的獨特性使其在新一代全球衛星導航系統中倍受青睞。

　　BOC調制信號經過導航衛星發射信道時，由于各個器件的非理想特性將會使其產生一定程度的失真，致使導航系統的性能會受到一定的影響。目前，國內外對此已有相關的研究。文獻主要分析Galileo的幾個候選BOC 調制信號特性，其中BOC 調制的非線性特性主要是采用固態功率放大器（SSPA）來仿真，分析了輸入功率回退（IBO）為0 dB時，BOC調制方式的相關損耗。文獻主要分析Galileo的幾個候選BOC調制信號的跟蹤精度受到線性和非線性失真的影響，分析了由于濾波器帶寬的限制而帶來的功率損耗和相關損耗。文獻主要分析星上高功放對BOC 及其衍生信號的失真影響，主要分析了帶寬限制和非線性效應帶來的聯合影響。

　　非線性失真對衛星導航系統性能的影響主要在于：引起信號幅度、相位失真，使星座圖發生壓縮偏轉，致使接收方判決檢測受很大影響，引起帶內失真；產生大量的互調失真和諧波失真，信號頻譜擴展產生的鄰道干擾（ACI），產生帶外失真。因此，對衛星導航信道的非線性補償研究顯得尤為重要。但是，目前國內外大部分只是針對非理想衛星信道對BOC信號的影響進行了研究，對于消除這種影響的研究卻甚少。

　　自適應數字預失真技術是補償非線性失真最好的方法之一，它通過在非線性器件前構造非線性失真的逆特性來達到線性化目的。隨著信息速率的增加，信號帶寬不斷增加，導航信道不僅具有非線性特性，其記憶效應也越來越明顯。對于有記憶效應的非線性失真，若仍采用傳統的無記憶預失真技術，非線性補償機制可能失效或是效果不佳。因此，研究記憶非線性失真的線性補償技術具有非常重要的意義。

　　本文即是對BOC 信號進行預失真仿真分析，對導航衛星發射信道進行建模等效，提出將發射信道等效為Wiener-Hammerstein模型，并設計了一種針對此模型的基于直接學習結構的自適應LMS 預失真方案，通過仿真結果可以看出該預失真方案可以很好地消除導航信道對BOC信號的失真影響。

　　1 導航發射信道模型

　　根據目前已有的國內外導航衛星發射信道模型，可歸納總結出導航衛星發射信道的等效簡化模型如圖1所示。

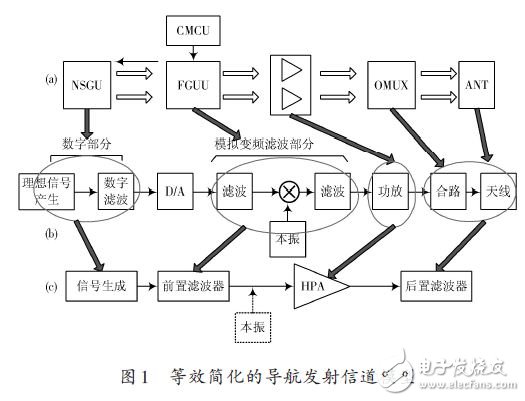
　　如圖1所示，前置濾波器和后置濾波器均采用線性FIR 濾波器，高功放采用行波管功率放大器（TWTA）模型。行波管大功率放大器AM/AM變換表現為幅度非線性失真，AM/PM變換表現為相位非線性失真，通常可用無記憶Saleh幅值-相位模型進行模擬，即：

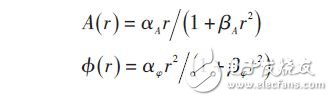
　　當綜合考慮前置濾波器、TWTA、后置濾波器時，記憶效應不能忽略，此時，導航發射信道實際上可以等效為有記憶Wiener-Hammerstein 模型，即線性時不變系統（LTI_1）后串連一個無記憶非線性模型（NL）后再串連一個線性時不變系統（LTI_2），該模型常用于描述衛星通信中的大功率功放。其結構圖如圖2所示。

　　其中每個模塊用數學表達式表示為：

　　綜合每個模塊可得Wiener-Hammerstein 模型的數學表達式為：

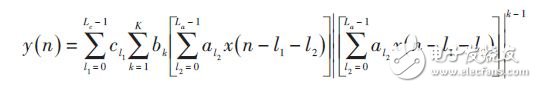
　　式中：K 表示功放模型的多項式階數；L 表示功放的記憶深度。

　　2 預失真方案

　　預失真方法通常分為查找表預失真和多項式預失真，因多項式預失真較節省RAM存儲單元，且收斂速度快，本文選用多項式預失真方法。基于多項式的預失真有直接學習結構和間接學習結構兩種，其中直接學習結構的結構簡單，算法收斂后能達到比較好的預失真效果，預失真器參數不受功放非線性系統輸出端噪聲的影響，可直接更新預失真器的參數。但需首先設定PA模型，根據模型估計出放大器的非線性傳遞函數，再求出逆函數作為預失真器的傳遞函數。由第一部分導航發射信道模型的描述可知，導航發射信道的主體部分可等效為有記憶Wiener-Hammerstein模型，符合直接學習結構中要求模型已知的條件，所以本文采用直接學習結構。

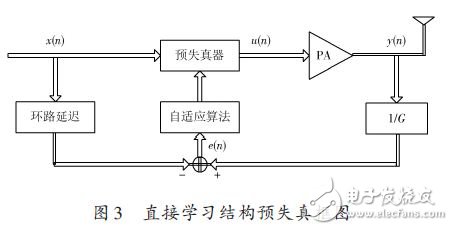
　　圖3即為基于直接學習結構的預失真框圖，在這個結構中，x（n） 為n 時刻的輸入信號，y（n） 為功放的輸出信號，其中整個系統所期望的響應為d（n），圖中的線性放大倍數為G，當e（n） = d（n） - y（n） 在算法收斂于e（n） = 0時，則功放的輸出為輸入信號的線性，并且有y（n） = G*x（n）。

　　針對本文建立的導航發射信道為一有記憶非線性信道，為補償非線性，其逆特性也應具有記憶效應。基于記憶多項式的預失真通常可以很好地補償有記憶效應的非線性模型，記憶多項式模型如下：

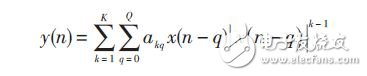
　　式中：K 為記憶多項式階數，補償效果與多項式階數有關，一定程度下，階數越高補償效果越好，但同時會增加算法的復雜度，針對相同的輸入信號，預失真多項式最佳階數的選擇與功放模型有關。Q 為記憶深度，記憶深度越大，預失真效果也越明顯，功放線性度改善越好，但太大也會實現困難，要根據實際需要選取合適的。

　　akq 是預失真器的多項式系數，其估計精度決定了預失真器的性能，系數更新可以通過自適應算法獲得。

　　LMS算法是一種梯度最速下降算法［8］，在算法迭代過程中，它不需要計算相應的相關矩陣，也不需要進行矩陣運算，因此具有每次迭代時的計算量最小，所用的存儲空間最少，容易以硬件實現，便于調試等優點，被廣泛應用。其算法流程圖如圖4所示。

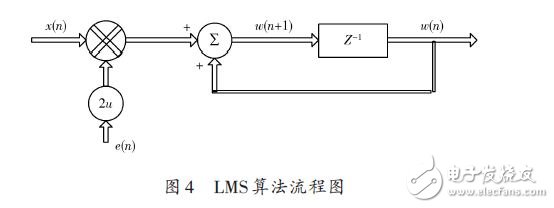
　　估計的誤差信號為：

　　可以看出，由當前時刻的權系數矢量和以誤差函數為比例因子的輸入矢量可以得到下一時刻的權系數矢量。預失真器通過以上給定的算法，不斷更新預失真器的參數，以達到對信道記憶非線性逆特性的逼近。

　　3 仿真結果與分析

　　本文采用BOC（14，2）信號進行仿真驗證。碼延遲和載波初相位均為0，Saleh 模型使用經典模型參數［2.158 7 1.151 7 4.003 3 9.104 0］，FIR 濾波器的系數取［0.769 2 0.153 8 0.076 9］。多項式階數取5，記憶深度取3.圖5（a）為原始輸入的BOC（14，2）信號的星座圖，圖5（b）為經過濾波器的線性、功放的非線性等失真后的星座圖，輸入信號為BOC 信號，帶寬較寬，衛星信道呈現出有記憶的非線性特性，理想星座經過信道后，如果不采用任何補償措施，可看到星座圖已出現扭曲，幅度失真且出現相位偏轉。圖5（c）為加入預失真之后的星座圖，可看到星座圖已得到改善，接近理想星座。

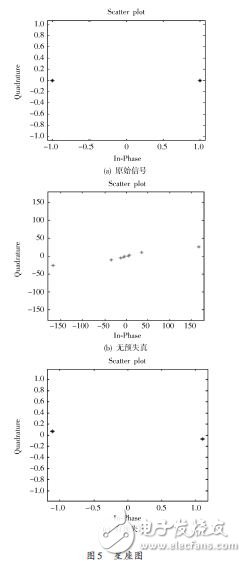
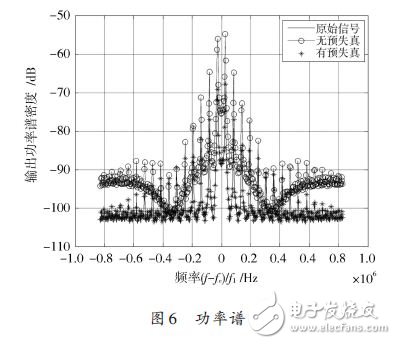
　　圖6 為BOC（14，2）信號在預失真前后系統輸出信號和原信號的功率譜密度，明顯可見，在經過衛星發射信道后信號不僅被放大且出現嚴重的帶外頻譜擴展，會造成相鄰信道干擾（ACI），引起帶外失真。在信號經過預失真后，明顯降低了BOC信號的帶外頻譜擴展，減少了相鄰信道干擾（ACI），大大減小了帶外失真。

　　4 結語

　　基于當前導航衛星發射信道的記憶非線性對BOC信號的失真影響，本文通過對導航衛星發射信道的等效簡化建模的研究，提出將發射信道的主體部分（HPA以及前后置濾波器）等效為有記憶Wiener-Hammerstein模型，并設計出一種適合此模型的基于直接學習結構的自適應LMS預失真方案，用于消除這種失真影響。仿真結果表明，該方案能有效抑制BOC信號的帶外頻譜擴展，減小帶外失真，優化星座圖，減小帶內失真，可以很好地消除導航信道對BOC 信號的失真影響，在衛星導航系統中有著重要的意義。