?

　　文章針對OFDM系統(tǒng)中存在的高峰均比提出了一些相關(guān)的抑制技術(shù)，提高了系統(tǒng)的可靠性和有效性。在實(shí)際應(yīng)用中，可根據(jù)要求和需要選擇適合的方法。

　　1 OFDM系統(tǒng)中峰均比的定義

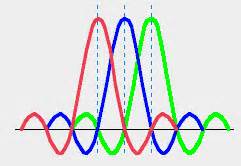
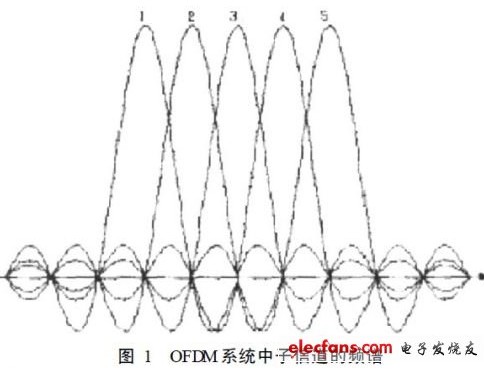
　　一個(gè)OFDM符號是由多個(gè)獨(dú)立的經(jīng)過調(diào)制的子載波信號相加而成，在某個(gè)時(shí)刻，若多個(gè)子載波以同一個(gè)方向進(jìn)行累加時(shí)，就會(huì)產(chǎn)生比較高的峰均功率比(Peak-to-Average Power Ratio,PAPR)，簡稱峰均比。對于包含N個(gè)子信道的OFDM系統(tǒng)來說，當(dāng)N個(gè)子信號都以相同的相位求和時(shí)，所得到的信號的峰值功率就會(huì)是平均功率的N倍。如圖1所示，在這個(gè)例子里，峰均功率是平均功率的16倍，其中所有子載波都受到相同數(shù)據(jù)符號的調(diào)制。

?

　　我們定義峰均比為OFDM的峰值功率和其平均功率之比，即：

?

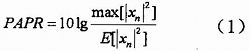
　　其中，xn表示在OFDM系統(tǒng)中經(jīng)過IFFT變換以后得到的輸出信號。基帶信號的峰均比可以表示為PART=10lgN，當(dāng)N=256時(shí)，PAPR=24dB，當(dāng)然這只是一個(gè)極端情況，OFDM系統(tǒng)內(nèi)的峰均比通常不會(huì)達(dá)到這一數(shù)值。

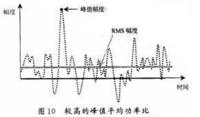
　　我們還用峰值系數(shù)(crest factor)來描述信號的峰值變化，該參數(shù)定義為最大信號值與方均根值之比：

?

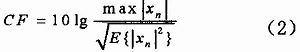
　　2 峰均比的性能衡量——CCDF函數(shù)

　　對于包含N個(gè)子載波的OFDM系統(tǒng)來說，其中經(jīng)過IFT計(jì)算得到的功率歸一化的復(fù)基帶信號是：

?

　　其中，Xk表示第k個(gè)子載波上的調(diào)制符號。對于OPSK來說，xk∈{1，-1，j，-j}。根據(jù)中心極限定理可知，只要子載波個(gè)數(shù)N足夠大，就可以判斷x(t)的實(shí)部和虛部都將遵循高斯分布，其均值為零，方差為0.5(實(shí)部和虛部各占整個(gè)信號功率的一半)。因此，可以得知，OFDM符號的幅值r服從瑞利分布，而其功率分布則要服從兩個(gè)自由度的中心耽分布，其中，均值為零，方差為1，由于自由度為二的中心x2，分布的概率密度函數(shù)為ppower(y)=e-y，因此，可以計(jì)算得到其累積分布函數(shù)(CDF，Cumulative Distribution Function)為：

?

　　當(dāng)然，也可以從另一個(gè)角度來衡量OFDM系統(tǒng)的PAPR分布，即計(jì)算峰均比超過某一個(gè)門限Z的概率，得到互補(bǔ)累計(jì)分布函數(shù)CCDF：

?

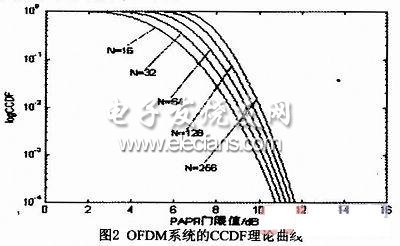
　　圖2是不同N數(shù)條件下，CCDF的理論曲線圖。從圖中可以看出，在給定PAPR門限值的條件下，N越大，出現(xiàn)高于門限值的概率也越大。

?

　　在隨后的討論中，一般都采用CCDF來衡量OFDM系統(tǒng)內(nèi)的PAPR分布。

　　3 國內(nèi)外對OFDM系統(tǒng)峰均比抑制的研究現(xiàn)狀

　　峰均比已成為OFDM技術(shù)研究的熱點(diǎn)之一，縱觀國內(nèi)外，人們已提出了大量的解決方案，主要分為這兩條途徑：一是提高功率放大器的性能，二是降低信號的峰均比。為了使高峰均比信號無失真地發(fā)射出去，功率放大器需要具有高度的線性和很大的回退(Back-off)，但是這樣的放大器功率效率很低。直流偏轉(zhuǎn)(Do Bias)方案可以提高放大器的功率效率，而線性化和預(yù)失真技術(shù)能通過改進(jìn)放大器的線性而減小放大器造成的非線性失真，以及改進(jìn)接收端的解碼性能，但是，這些技術(shù)并不能從根本上解決多載波信號的高PAPR給放大器帶來的難題。而降低信號的PAPR可以說是從本質(zhì)上來解決多載波系統(tǒng)的高PAPR問題，目前，研究者已經(jīng)提出了許多方案，可以大致歸為信號預(yù)畸變、編碼技術(shù)和擾碼三類。

　　預(yù)畸變技術(shù)是最早采用的方法，由于較大峰值出現(xiàn)的概率非常小，因此，預(yù)畸變技術(shù)是一種非常直接和有效的降低PAPR的方法，但是它將導(dǎo)致嚴(yán)重的帶內(nèi)干擾和帶外噪聲，從而降低整個(gè)系統(tǒng)的誤碼性能和頻譜效率。編碼類技術(shù)降PAPR為線性過程，它不會(huì)使信號產(chǎn)生畸變，因此沒有限幅類技術(shù)的缺點(diǎn)，但編碼類技術(shù)的計(jì)算復(fù)雜度非常高，編解碼都比較麻煩，而且這類技術(shù)的信息速率降低很快，因此，只適用于子載波數(shù)比較少的情況;擾碼技術(shù)能有效降低信號的PAPR，其缺點(diǎn)也是計(jì)算復(fù)雜度太大，但到目前為止，已有很多有效的方法來減少計(jì)算的復(fù)雜度。因此，在這三類技術(shù)中，擾碼技術(shù)最有希望解決OFDM中的PAPR問題。下面將對這三類技術(shù)進(jìn)行詳細(xì)的介紹。

　　3.1 信號預(yù)畸變技術(shù)

　　信號預(yù)畸變技術(shù)是最簡單也是最直接的降低OFDM系統(tǒng)中PAPR的方法。在信號被送到放大器之前，首先經(jīng)過非線性處理，對有較大峰值功率的信號進(jìn)行預(yù)畸變，使其不會(huì)超出放大器的動(dòng)態(tài)變化范圍，從而避免較大PAPR的出現(xiàn)。最常用的信號預(yù)畸變技術(shù)包括限幅加窗技術(shù)和壓縮擴(kuò)展技術(shù)。

　　3.1.1 限幅技術(shù)

　　限幅技術(shù)就是信號在經(jīng)過非線性部件之前進(jìn)行限幅，使得峰值信號低于所期望的最大電平值。盡管限幅方法十分簡單，但也會(huì)給OFDM系統(tǒng)帶來相應(yīng)的一些問題：首先，對OFDM符號的幅度進(jìn)行畸變，會(huì)對系統(tǒng)造成自身的于擾，從而導(dǎo)致系統(tǒng)的誤碼率性能降低。其次，OFDM信號的非線性畸變會(huì)導(dǎo)致帶外輻射功率的增加，因?yàn)橄薹倪^程是將OFDM符號乘以一個(gè)矩形濾波器，將高于某個(gè)幅度的波形削平，因此限幅后的帶寬是由兩者的帶寬共同決定的。為了克服矩形窗函數(shù)所造成的帶外輻射過大的問題，可以利用其它的非矩形窗函數(shù)，例如Gaussian窗、Co-sine窗、Kaiser窗以及Hamming窗等。總的來說，選擇窗函數(shù)的原則為：頻譜特性要好，不能在時(shí)域內(nèi)過長以避免對更多的時(shí)域采樣信號造成影響。

　　3.1.2 壓擴(kuò)變換技術(shù)

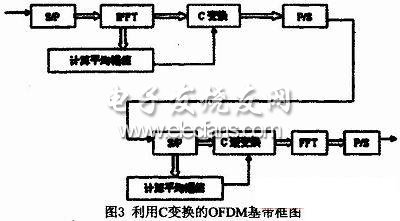
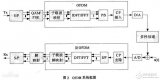
　　預(yù)畸變減小PAPR的壓擴(kuò)變換(C變換)技術(shù)的主要思想是：把大功率發(fā)射信號進(jìn)行壓縮，而把小功率信號進(jìn)行放大，從而使發(fā)射信號的平均功率相對保持不變，這樣不但可以減小系統(tǒng)的PAPR，而且還可以提高系統(tǒng)的抗干擾能力。在發(fā)射端對信號進(jìn)行壓擴(kuò)，而在接收端要實(shí)施逆操作，其優(yōu)點(diǎn)是減小PAPR，增強(qiáng)小功率信號抗干擾的能力。C變換的基本過程如圖3所示。

?

　　OFDM系統(tǒng)輸出符號的復(fù)基帶信號可以表示為：

?

　　其中T表示OFDM信號周期長度，k表示一個(gè)符號周期內(nèi)第k個(gè)采樣值，n表示時(shí)域內(nèi)的第n個(gè)OFDM符號。g(t)表示滿足Nyquist脈沖濾波器的沖擊響應(yīng)，Sn，k表示經(jīng)過變換的第n個(gè)OFDM符號中的第k個(gè)采樣值，即Sn,k=C{xn,k}，其中xn,k表示經(jīng)過IFFT變換后的OFDM信號，C{.}表示壓縮變換，并且這種變換滿足以下兩個(gè)條件：

　　(1)當(dāng)|x|≤，|C{X}|≥|x|;否則，|C{X}|≤|x|，其中m表示C變化的轉(zhuǎn)折點(diǎn);

　　(2)滿足E{|X|2}≈E{|C{x}|2}，即保持變換前后的平均功率大致相等。

　　由此可以看到，若能適當(dāng)?shù)剡x擇C變換的形式以及轉(zhuǎn)折點(diǎn)m，就可以顯著地改善PAPR性能，并且沒有太多增加系統(tǒng)的復(fù)雜度。需要注意的是，如果平均幅值等于C變換的轉(zhuǎn)折點(diǎn)，并且C變換能夠滿足關(guān)于轉(zhuǎn)折點(diǎn)呈現(xiàn)奇對稱，就可以保證發(fā)送信號的平均功率經(jīng)過C變換后基本保持不變。為滿足上面的要求，C變換可以用下面的公式表示：

?

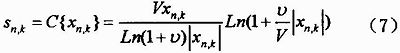
　　其中，xn,k表示OFDM信號xn,k的平均幅值，也就是C變換的轉(zhuǎn)折點(diǎn)ν一般取小于5，在接收端可以對信號rn，k實(shí)施C逆變換，即

?

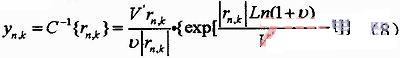
　　其中V’表示接收信號rn,k的平均幅值。圖4給出了利用C變換所得到的OFDM系統(tǒng)的CCDF與PAPR的示意圖：

?

　　3.2 擾碼技術(shù)

　　這類技術(shù)的基本思想并不是要降低信號幅度的最大值，而是降低峰值出現(xiàn)的概率。它是通過對原OFDM符號作線形分割和線形交換，以減少信號峰值出現(xiàn)的概率，優(yōu)化子信道的載波相位以尋找能得到最低PAPR的相位組合。一般的模式是在發(fā)送端對每一個(gè)OFDM符號，根據(jù)某些規(guī)則產(chǎn)生多個(gè)候選的時(shí)域波形，并計(jì)算每一波形的PAPR，最終傳輸PAPR最小的那一個(gè)。這種方法雖然并不能保證所有傳輸信號的幅度都小于門限值，但是卻大大降低了峰值出現(xiàn)的概率，也就降低了限幅噪聲對系統(tǒng)帶來的不利影響。它在結(jié)構(gòu)上容易實(shí)現(xiàn)，應(yīng)用靈活，是目前最具應(yīng)用潛力也是最為熱門的方案。這里主要介紹選擇性映射(SLM)和部分傳輸序列方法(PTS)兩種方法。

　　3.2.1 選擇性映射

　　OFDM系統(tǒng)發(fā)射機(jī)內(nèi)的信號可以表示為：xk=IFFT[Xn]，(n,k=0，…，N-1)。假設(shè)存在M個(gè)不同的、長度為N的隨機(jī)相位序列矢量(Pμ=p0(μ)，…，pN-1μ)，其中(μ=0，…，M-1)，pi(μ)=exp(jφi(μ))，φi(μ)在[0，2π]之內(nèi)均勻分布。可以利用這朋個(gè)相位矢量分別與IFFT的輸入序列x進(jìn)行點(diǎn)乘，則可以得到M個(gè)不同的輸出序列X(μ)間，即：

?

　　其中(·)表示向量之間的點(diǎn)乘。然后對所得到的M個(gè)序列X(μ)分別實(shí)施IFFT計(jì)算，相應(yīng)得到M個(gè)不同的輸出序列X(μ)=(X0(μ)，…，XN-1(μ))。最后在給定PAPR門限值的條件下，從這個(gè)M個(gè)時(shí)域信號序列內(nèi)選擇PAPR性能最好的用于傳輸。

　　SLM方法的原理框圖如圖5所示。

?

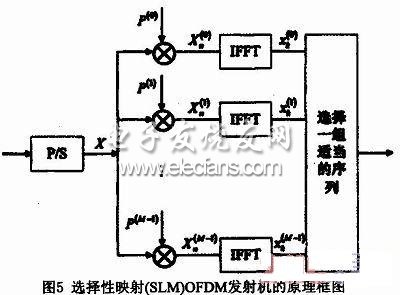
　　設(shè)峰均比的門限值為PAPR0，則原始OFDM序列的PAPR超過門限值的概率定義為Pr{PAPR>PAPR0};而這M個(gè)序列x(μ)，(μ=0，…，M-1)的PAPR都超過門限值的概率就會(huì)變?yōu)閇PT{PAPR>PAPR0}]M，根據(jù)式(5)可以計(jì)算出SLM-OFDM系統(tǒng)內(nèi)PAPR的CCDF為：

?

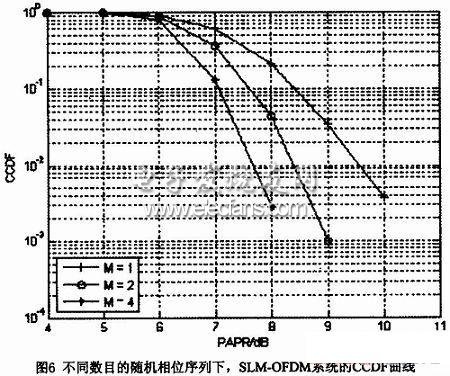
　　其中M=1時(shí)，就是原始OFDM系統(tǒng)PAPR分布的CCDF。圖6表示了子載波數(shù)為128時(shí)，不同肘取值下，OFDM系統(tǒng)采用SLM算法PAPR的CCDF曲線。

　　這種算法的缺點(diǎn)是需要額外計(jì)算M-1組的IFFT運(yùn)算，且接收機(jī)必須知道選擇的相位。

?

　　3.2.2 部分傳輸序列方法(PTS)

　　PTS是另外一種常用的減小OFDM系統(tǒng)PAPR的方法，其主要思想為將輸入數(shù)據(jù)符號分成若干組，然后再合并這些分組，以此來減小以PA-PR。

　　首先利用向量來定義數(shù)據(jù)符號X=(X0，X1，…，XN-1)，然后把向量X割成V組，分別由(Xv,V=1，2，…，V}來表示，其分割方法可以有多種。假設(shè)每個(gè)分組中所包含的N數(shù)是相同的，然后將這階分組按照如下的方法組合起來：

?

　　其中，{bv,V=1，2，…，V}是加權(quán)系數(shù)，且滿足bv=exp(jφv)以及φv∈[0，2π]，這些被稱為輔助信息(Side Information)。之后再對X’進(jìn)行IFFT變換，得到x’=IFFT{X’}。再根據(jù)公式(11)及參考IFFT變換的線性，利用V個(gè)單獨(dú)的IFFT變換，對各個(gè)分組進(jìn)行計(jì)算，最終得到下式：

?

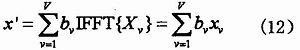
　　其中引入了V個(gè)部分發(fā)送序列xv=IFFT{Xv}。可以通過適當(dāng)?shù)剡x擇輔助加權(quán)系數(shù)(bv,V=1，2，…，V}，從而使上式的峰值信號到達(dá)最佳。

　　為使OFDM系統(tǒng)內(nèi)的PAPR最優(yōu)的最優(yōu)加權(quán)系數(shù)應(yīng)滿足下面的公式：

?

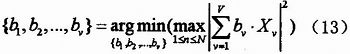
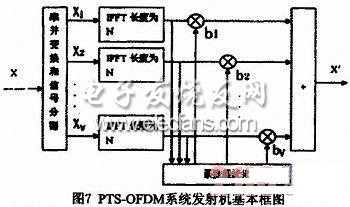
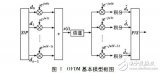
　　其中，argmin(.)表示函數(shù)取得最小值時(shí)所使用的判決條件。這樣一來，就可以以V-1次IFFT計(jì)算為代價(jià)，通過尋找最佳的{bv，V=1，2，…，V}系數(shù)，使得OFDM系統(tǒng)內(nèi)的PAPR性能得到較好的改善。圖7給出了采用PTS方法的基本框圖。

?

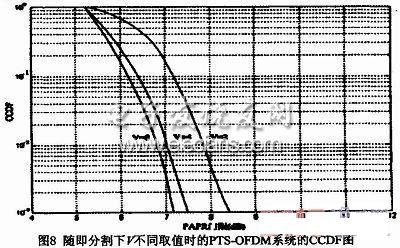
　　這種算法與SLM有著共同的缺點(diǎn)，那就是大大增加了系統(tǒng)的復(fù)雜度，導(dǎo)致計(jì)算量也大大增加。可以通過限制bv的取值范圍和采用適當(dāng)?shù)姆指钷k法來降低復(fù)雜度。分割方法主要有隨即分割、交織分割、相鄰分割。圖8給出了用隨即分割方法在V取不同值時(shí)的PTS-OFDM的CCDF曲線：

?

　　3.3 編碼技術(shù)

　　編碼技術(shù)的基本思想是利用編碼方法來產(chǎn)生PAPR較小的OFDM符號。其核心是運(yùn)用一種特殊的前向糾錯(cuò)技術(shù)除掉高PAPR的OFDM信號。典型的碼組有分組碼、M序列、格雷(Golay)碼和雷德密勒(Reed-Muller)碼等。下面對上述的幾種方法進(jìn)行簡單的介紹。

　　(1)分組編碼。其基本思想是：在對比特流進(jìn)行IFFT運(yùn)算之前，先進(jìn)行特殊的編碼處理(如應(yīng)用奇偶校驗(yàn)位)，使得輸出的比特流經(jīng)過OFDM調(diào)制后具有較低的PAPR。精心設(shè)計(jì)的分組編碼方法不僅可以有效地降低PAPR，同時(shí)還可以起到類似于信道編碼的作用，使系統(tǒng)具有前向檢錯(cuò)和糾錯(cuò)的能力。

　　(2)M序列。該序列具有良好的自相關(guān)性，因此將其作為IFFT的輸入，得到的信號就會(huì)具有很低的PAPR。用M序列對輸入信息進(jìn)行編碼可以將OFDM信號的PAPR限制在5-7dB。

　　(3)格雷互補(bǔ)序列。把GCS作為IFFT的輸入，那么它的輸出信號就會(huì)有比較低的PAPR值。應(yīng)用GCS序列的最大優(yōu)點(diǎn)就是不論子載波數(shù)多少，其PAPR至多為3dB。但是，由于隨著子載波數(shù)的逐漸增多，尋找最佳生成矩陣具有相當(dāng)高的難度，因此格雷互補(bǔ)序列碼并不適用于載波數(shù)較大的OFDM系統(tǒng)。

　　(4)雷德密勒碼。一種高效的編碼方案，具有一定的糾錯(cuò)性能。利用RM碼與GCS碼構(gòu)造新的分組編碼，此分組碼同時(shí)具有GCS和RM碼的性能，不僅可將PAPR降至3dB以內(nèi)，同時(shí)還具有良好的糾錯(cuò)檢錯(cuò)能力。

　　應(yīng)用編碼方法降低PAPR的優(yōu)點(diǎn)是系統(tǒng)相對簡單、穩(wěn)定，且降低PAPR的效果好。但它的缺點(diǎn)也非常明顯：一是受編碼調(diào)制方式的限制，比如分組編碼就只能適用于PSK調(diào)制方式，而不適用于基于QAM調(diào)制方式的OFDM系統(tǒng);二是受限于子載波數(shù)，隨著子載波數(shù)的增加，計(jì)算復(fù)雜度增大，系統(tǒng)的吞吐量嚴(yán)重下降，帶寬的利用率顯著降低等;三是數(shù)據(jù)的編碼速率有所減小，因?yàn)榇蟛糠值木幋a方法都要引入一定的冗余信息。

　　4 小結(jié)

　　OFDM系統(tǒng)具有較大的PAPR，它直接影響著整個(gè)系統(tǒng)的運(yùn)行成本和效率，也是影響OFDM技術(shù)在未來移動(dòng)通信系統(tǒng)中應(yīng)用的關(guān)鍵因素之一。

　　本文首先針對OFDM系統(tǒng)內(nèi)PAPR的定義和它的性能衡量函數(shù)(CCDF)進(jìn)行討論，然后對降低OFDM系統(tǒng)PAPR問題的3類技術(shù)進(jìn)行分析，包括限幅類技術(shù)、擾碼技術(shù)和編碼技術(shù)。限幅類技術(shù)分析了直接限幅方法和壓擴(kuò)變換技術(shù);擾碼類技術(shù)介紹了兩種具有代表性的技術(shù)：選擇性映射(SLM)和部分傳輸序列(PTS)，并分析了各自降PAPR的原理和優(yōu)缺點(diǎn);編類碼技術(shù)簡單介紹了它的原理和幾種主要的方法。這3類方法都有各自的著眼點(diǎn)和特色，也都存在著缺陷。限幅類技術(shù)直接對信號的峰值進(jìn)行非線性操作，它最直接，最簡單。但因?yàn)樗捎昧朔蔷€性操作，因此會(huì)帶來帶內(nèi)噪聲和帶外干擾，從而降低系統(tǒng)的誤碼率性能和頻譜效率。編碼技術(shù)利用編碼將原來的信息碼字映射到一個(gè)具有比較好的PAPR特性的傳輸碼集上，從而避開了那些會(huì)出現(xiàn)信號峰值的碼字。該類技術(shù)為線性過程，它不會(huì)使信號產(chǎn)生畸變，因此也沒有限幅類技術(shù)的缺點(diǎn)。但是，編碼技術(shù)的計(jì)算復(fù)雜度非常高，編解碼都非常麻煩。更重要的是，這類技術(shù)的信息速率降低得很快，因此只適用于子載波數(shù)比較少的情況。至于擾碼類技術(shù)，它不像編碼技術(shù)完全避開信號的峰值，而是著眼于努力使信號峰值出現(xiàn)的概率降低。這類技術(shù)采用的方法也為線性過程，因此它不會(huì)對信號產(chǎn)生畸變。這類技術(shù)能夠有效地降低信號的PAPR值，它的缺點(diǎn)也是計(jì)算復(fù)雜度太大。在實(shí)際應(yīng)用中，應(yīng)根據(jù)系統(tǒng)性能要求和實(shí)際需要，選擇適合的方法。