什么是巴特沃斯濾波器
巴特沃斯濾波器是電子濾波器的一種。巴特沃斯濾波器的特點是通頻帶的頻率響應(yīng)曲線最平滑。這種濾波器最先由英國工程師斯替芬·巴特沃斯(StephenButterworth)在1930年發(fā)表在英國《無線電工程》期刊的一篇論文中提出的。巴特沃斯濾波器的振幅對角頻率單調(diào)下降,并且也是唯一的無論階數(shù),振幅對角頻率曲線都保持同樣的形狀的濾波器。巴特沃斯濾波器的特點是通頻帶內(nèi)的頻率響應(yīng)曲線最大限度平坦,沒有起伏,而在阻頻帶則逐漸下降為零。二階巴特沃斯濾波器的衰減率為每倍頻12分貝、三階巴特沃斯濾波器的衰減率為每倍頻18分貝、如此類推。
巴特沃斯濾波器特性
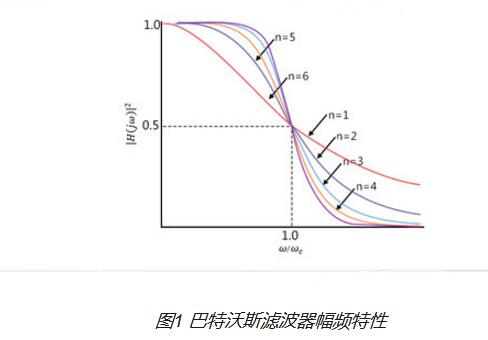
巴特沃斯濾波器的特點是通頻帶內(nèi)的頻率響應(yīng)曲線最大限度平坦,沒有起伏,而在阻頻帶則逐漸下降為零。在振幅的對數(shù)對角頻率的波特圖上,從某一邊界角頻率開始,振幅隨著角頻率的增加而逐步減少,趨向負無窮大。
一階巴特沃斯濾波器的衰減率為每倍頻6分貝,每十倍頻20分貝。二階巴特沃斯濾波器的衰減率為每倍頻12分貝、三階巴特沃斯濾波器的衰減率為每倍頻18分貝、如此類推。巴特沃斯濾波器的振幅對角頻。單調(diào)下降,并且也是唯一的無論階數(shù),振幅對角頻率曲線都保持同樣的形狀的濾波器。只不過濾波器階數(shù)越高,在阻頻帶振幅衰減速度越快。其他濾波器高階的振幅對角頻率圖和低級數(shù)的振幅對角頻率有不同的形狀。
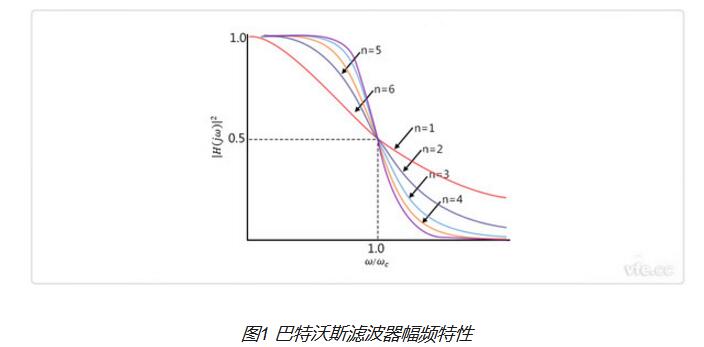
巴特沃斯濾波器原理
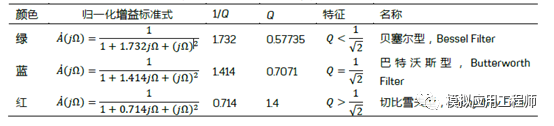
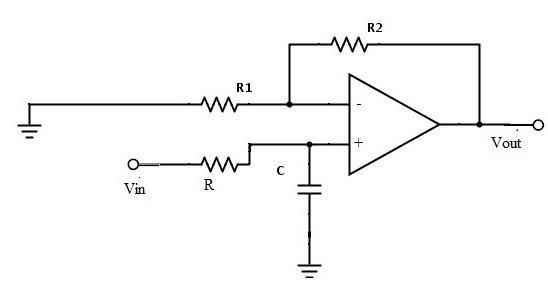
巴特沃斯型濾波器在現(xiàn)代設(shè)計方法設(shè)計的濾波器中,是最為有名的濾波器,由于它設(shè)計簡單,性能方面又沒有明顯的缺點,又因它對構(gòu)成濾波器的元件Q值較低,因而易于制作且達到設(shè)計性能,因而得到了廣泛應(yīng)用。其中,巴特沃斯濾波器的特點是通頻帶的頻率響應(yīng)曲線最平滑。
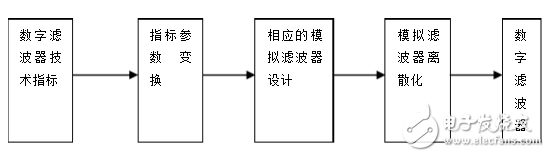
濾波器的截止頻率的變換是通過先求出待設(shè)計濾波器的截止頻率與基準(zhǔn)濾波器的截止頻率的比值M,再用這個M去除濾波器中的所有元件值來實現(xiàn)的,其計算公式如下:M=待設(shè)計濾波器的截止頻率/基準(zhǔn)濾波器的截止頻率。
濾波器的特征阻抗的變換是通過先求出待設(shè)計濾波器的特征阻抗與基準(zhǔn)濾波器的特征阻抗的比值K,再用這個K去乘基準(zhǔn)濾波器中的所有電感元件值和用這個K去除基準(zhǔn)濾波器中的所有電容元件值來實現(xiàn)的。
巴特沃斯濾波器與其它濾波器比較
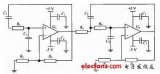
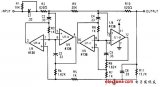
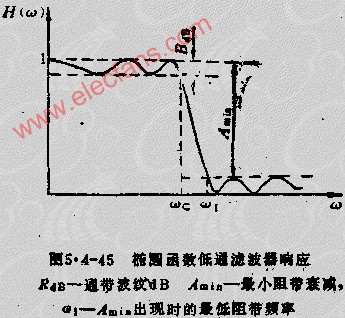
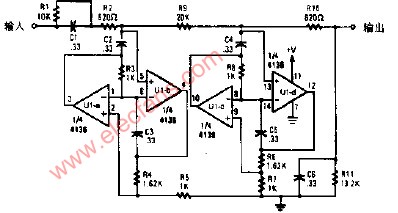
下圖是巴特沃斯濾波器(左上)和同階第一類切比雪夫濾波器(右上)、第二類切比雪夫濾波器(左下)、橢圓函數(shù)濾波器(右下)的頻率響應(yīng)圖。
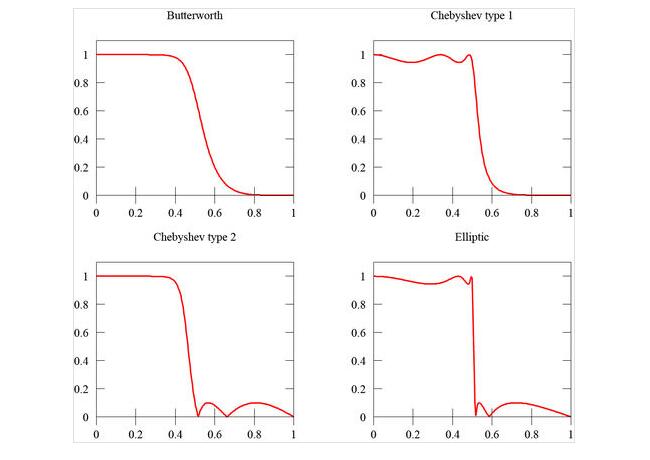
特沃斯濾波器優(yōu)點
巴特沃斯濾波器的特點是通頻帶內(nèi)的頻率響應(yīng)曲線最大限度平坦,沒有起伏,而在阻頻帶則逐漸下降為零。在振幅的對數(shù)對角頻率的波得圖上,從某一邊界角頻率開始,振幅隨著角頻率的增加而逐漸減少,趨向負無窮大。
一階巴特沃斯濾波器的衰減率為每倍頻6分貝,每十倍頻20分貝。二階巴特沃斯濾波器的衰減率為每倍頻12分貝,三階巴特沃斯濾波器的衰減率為每倍頻18分貝,如此類推。巴特沃斯濾波器的振幅對角頻率單調(diào)下降,并且也是唯一的無論階數(shù)、振幅對角頻率曲線都保持同樣的形狀的濾波器。只不過濾波器階數(shù)越高,在阻頻帶振幅衰減速度越快。其他濾波器高階的振幅對角頻率圖和低級數(shù)的振幅對角頻率有不同的形狀。
巴特沃斯濾波器是濾波器的一種設(shè)計分類,類同于切比雪夫濾波器,它有高通,低通,帶通,高通,帶阻等多種濾波器。它在通頻帶內(nèi)外都有平穩(wěn)的幅頻特性,但有較長的過渡帶,在過渡帶上很容易造成失真,我在調(diào)用MATLAB里的巴特沃斯濾波器做仿真時,信號總會在第一個周期略微有些失真,但往后的幅頻特性就非常的好。
巴特沃斯濾波器主要參數(shù)介紹
(1)[N,wc]=buttord(wp,ws,RP,As,’s’)
該格式用于計算巴特沃斯模擬濾波器的階數(shù)N和3db截止頻率wc。Wp、ws和wc是實際模擬角頻率(rad\s)。Rp和As為通帶最大衰減和最小衰減。
(2)[Z,P,k]=buttap(N)
該格式用于計算N階巴特沃斯歸一化模擬低通原型濾波器系統(tǒng)函數(shù)的零、極點和增益因子,返回長度為N的列向量Z和P,分別給出N個零點和極點的位置,K表示濾波器增益。
(3)Y=filter(b,a,x)
式中b表示系統(tǒng)傳遞函數(shù)的分子多項式的系數(shù)矩陣;a表示系統(tǒng)傳遞函數(shù)的分母多項式的系數(shù)矩陣;x表示輸入序列;filter表示輸出序列。IIR函數(shù)實現(xiàn)的直接形式。
(4)[b,a]=butter(N,wc,‘ftype’)
計算N階巴特沃斯數(shù)字濾波器系統(tǒng)函數(shù)分子、分母多項式的系數(shù)向量b、a。
說明:調(diào)用參數(shù)N和wc分別為巴特沃斯數(shù)字濾波器的階數(shù)和3dB截止頻率的歸一化值,一般是調(diào)用buttord格式(1)計算N和wc。系數(shù)b、a是按照z-1的升冪排列。
(5)[B,A]=butter(N,Ωc,‘ftype’,‘s’)
計算巴特沃斯模擬濾波器系統(tǒng)函數(shù)的分子、分母多項式系數(shù)向量。
說明:調(diào)用參數(shù)N和Ωc分別為巴特沃斯模擬濾波器的階數(shù)和3dB截止頻率(實際角頻率),可調(diào)用buttord(2)格式計算N和Ωc。系數(shù)B、A按s的正降冪排列。
tfype為濾波器的類型:
◇ftype=high時,高通;Ωc只有1個值。
◇ftype=stop時,帶阻;Ωc=[Ωcl,Ωcu],分別為帶阻濾波器的通帶3dB下截止頻率和上截止頻率。
◇ftype缺省時:若Ωc只有1個值,則默認為低通;若Ωc有2個值,則默認為帶通;其通帶頻率區(qū)間Ωcl《Ω《Ωcu。
(6)[H,w]=freqz(b,a,N)
b和a分別為離散系統(tǒng)的系統(tǒng)函數(shù)分子、分母多項式的系數(shù)向量,返回量H則包含了離散系統(tǒng)頻響在0~pi范圍內(nèi)N個頻率等分點的值(其中N為正整數(shù)),w則包含了范圍內(nèi)N個頻率等分點。調(diào)用默認的N時,其值是512。可以先調(diào)用freqz()函數(shù)計算系統(tǒng)的頻率響應(yīng),然后利用abs()和angle()函數(shù)及plot()函數(shù),繪制出系統(tǒng)的頻響曲線。
(7)lp2lp函數(shù)
[bt,at]=lp2lp(b,a,w0)
該函數(shù)用于實現(xiàn)由低通模擬原型濾波器至低通濾波器的頻率變換,可以用傳遞函數(shù)和狀態(tài)空間進行轉(zhuǎn)換,但無論哪種形式,其輸入必須是模擬濾波器原型。
(8)[bz,az]=impinvar(b,a,fs)
把具有[b,a]模擬濾波器傳遞函數(shù)模型轉(zhuǎn)換為采樣頻率為fs的數(shù)字濾波器的傳遞函數(shù)模型[bz,az],如果在函數(shù)中沒有確定頻率fs時,函數(shù)默認為1Hz.
 電子發(fā)燒友App
電子發(fā)燒友App









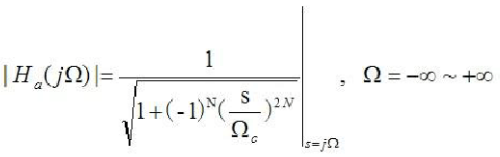












評論