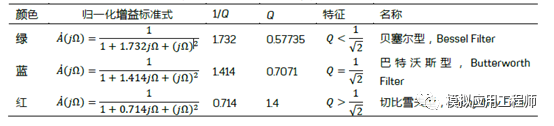
什么是巴特沃斯濾波器
巴特沃斯濾波器是電子濾波器的一種。巴特沃斯濾波器的特點是通頻帶的頻率響應曲線最平滑。這種濾波器最先由英國工程師斯替芬·巴特沃斯(StephenButterworth)在1930年發表在英國《無線電工程》期刊的一篇論文中提出的。巴特沃斯濾波器的振幅對角頻率單調下降,并且也是唯一的無論階數,振幅對角頻率曲線都保持同樣的形狀的濾波器。巴特沃斯濾波器的特點是通頻帶內的頻率響應曲線最大限度平坦,沒有起伏,而在阻頻帶則逐漸下降為零。二階巴特沃斯濾波器的衰減率為每倍頻12分貝、三階巴特沃斯濾波器的衰減率為每倍頻18分貝、如此類推。
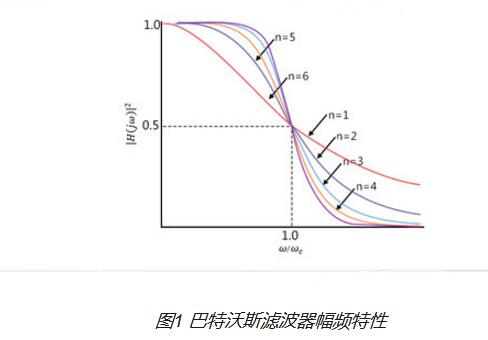
巴特沃斯濾波器特性
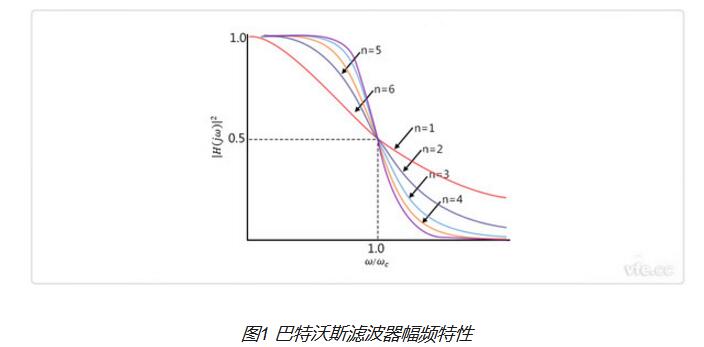
巴特沃斯濾波器的特點是通頻帶內的頻率響應曲線最大限度平坦,沒有起伏,而在阻頻帶則逐漸下降為零。在振幅的對數對角頻率的波特圖上,從某一邊界角頻率開始,振幅隨著角頻率的增加而逐步減少,趨向負無窮大。
一階巴特沃斯濾波器的衰減率為每倍頻6分貝,每十倍頻20分貝。二階巴特沃斯濾波器的衰減率為每倍頻12分貝、三階巴特沃斯濾波器的衰減率為每倍頻18分貝、如此類推。巴特沃斯濾波器的振幅對角頻。單調下降,并且也是唯一的無論階數,振幅對角頻率曲線都保持同樣的形狀的濾波器。只不過濾波器階數越高,在阻頻帶振幅衰減速度越快。其他濾波器高階的振幅對角頻率圖和低級數的振幅對角頻率有不同的形狀。
巴特沃斯濾波器原理
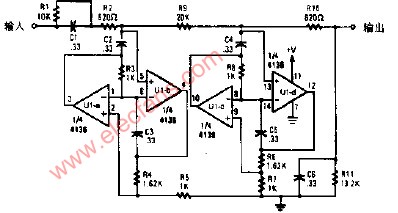
巴特沃斯型濾波器在現代設計方法設計的濾波器中,是最為有名的濾波器,由于它設計簡單,性能方面又沒有明顯的缺點,又因它對構成濾波器的元件Q值較低,因而易于制作且達到設計性能,因而得到了廣泛應用。其中,巴特沃斯濾波器的特點是通頻帶的頻率響應曲線最平滑。
濾波器的截止頻率的變換是通過先求出待設計濾波器的截止頻率與基準濾波器的截止頻率的比值M,再用這個M去除濾波器中的所有元件值來實現的,其計算公式如下:M=待設計濾波器的截止頻率/基準濾波器的截止頻率。
濾波器的特征阻抗的變換是通過先求出待設計濾波器的特征阻抗與基準濾波器的特征阻抗的比值K,再用這個K去乘基準濾波器中的所有電感元件值和用這個K去除基準濾波器中的所有電容元件值來實現的。
巴特沃斯濾波器與其它濾波器比較
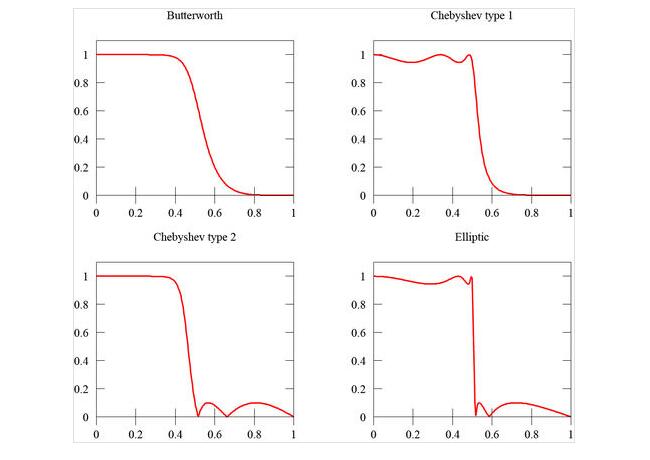
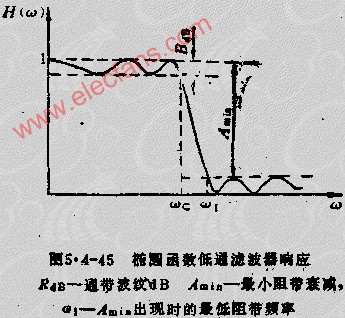
下圖是巴特沃斯濾波器(左上)和同階第一類切比雪夫濾波器(右上)、第二類切比雪夫濾波器(左下)、橢圓函數濾波器(右下)的頻率響應圖。
特沃斯濾波器優點
巴特沃斯濾波器的特點是通頻帶內的頻率響應曲線最大限度平坦,沒有起伏,而在阻頻帶則逐漸下降為零。在振幅的對數對角頻率的波得圖上,從某一邊界角頻率開始,振幅隨著角頻率的增加而逐漸減少,趨向負無窮大。
一階巴特沃斯濾波器的衰減率為每倍頻6分貝,每十倍頻20分貝。二階巴特沃斯濾波器的衰減率為每倍頻12分貝,三階巴特沃斯濾波器的衰減率為每倍頻18分貝,如此類推。巴特沃斯濾波器的振幅對角頻率單調下降,并且也是唯一的無論階數、振幅對角頻率曲線都保持同樣的形狀的濾波器。只不過濾波器階數越高,在阻頻帶振幅衰減速度越快。其他濾波器高階的振幅對角頻率圖和低級數的振幅對角頻率有不同的形狀。
巴特沃斯濾波器是濾波器的一種設計分類,類同于切比雪夫濾波器,它有高通,低通,帶通,高通,帶阻等多種濾波器。它在通頻帶內外都有平穩的幅頻特性,但有較長的過渡帶,在過渡帶上很容易造成失真,我在調用MATLAB里的巴特沃斯濾波器做仿真時,信號總會在第一個周期略微有些失真,但往后的幅頻特性就非常的好。
巴特沃斯濾波器主要參數介紹
(1)[N,wc]=buttord(wp,ws,RP,As,’s’)
該格式用于計算巴特沃斯模擬濾波器的階數N和3db截止頻率wc。Wp、ws和wc是實際模擬角頻率(rad\s)。Rp和As為通帶最大衰減和最小衰減。
(2)[Z,P,k]=buttap(N)
該格式用于計算N階巴特沃斯歸一化模擬低通原型濾波器系統函數的零、極點和增益因子,返回長度為N的列向量Z和P,分別給出N個零點和極點的位置,K表示濾波器增益。
(3)Y=filter(b,a,x)
式中b表示系統傳遞函數的分子多項式的系數矩陣;a表示系統傳遞函數的分母多項式的系數矩陣;x表示輸入序列;filter表示輸出序列。IIR函數實現的直接形式。
(4)[b,a]=butter(N,wc,‘ftype’)
計算N階巴特沃斯數字濾波器系統函數分子、分母多項式的系數向量b、a。
說明:調用參數N和wc分別為巴特沃斯數字濾波器的階數和3dB截止頻率的歸一化值,一般是調用buttord格式(1)計算N和wc。系數b、a是按照z-1的升冪排列。
(5)[B,A]=butter(N,Ωc,‘ftype’,‘s’)
計算巴特沃斯模擬濾波器系統函數的分子、分母多項式系數向量。
說明:調用參數N和Ωc分別為巴特沃斯模擬濾波器的階數和3dB截止頻率(實際角頻率),可調用buttord(2)格式計算N和Ωc。系數B、A按s的正降冪排列。
tfype為濾波器的類型:
◇ftype=high時,高通;Ωc只有1個值。
◇ftype=stop時,帶阻;Ωc=[Ωcl,Ωcu],分別為帶阻濾波器的通帶3dB下截止頻率和上截止頻率。
◇ftype缺省時:若Ωc只有1個值,則默認為低通;若Ωc有2個值,則默認為帶通;其通帶頻率區間Ωcl《Ω《Ωcu。
(6)[H,w]=freqz(b,a,N)
b和a分別為離散系統的系統函數分子、分母多項式的系數向量,返回量H則包含了離散系統頻響在0~pi范圍內N個頻率等分點的值(其中N為正整數),w則包含了范圍內N個頻率等分點。調用默認的N時,其值是512。可以先調用freqz()函數計算系統的頻率響應,然后利用abs()和angle()函數及plot()函數,繪制出系統的頻響曲線。
(7)lp2lp函數
[bt,at]=lp2lp(b,a,w0)
該函數用于實現由低通模擬原型濾波器至低通濾波器的頻率變換,可以用傳遞函數和狀態空間進行轉換,但無論哪種形式,其輸入必須是模擬濾波器原型。
(8)[bz,az]=impinvar(b,a,fs)
把具有[b,a]模擬濾波器傳遞函數模型轉換為采樣頻率為fs的數字濾波器的傳遞函數模型[bz,az],如果在函數中沒有確定頻率fs時,函數默認為1Hz.
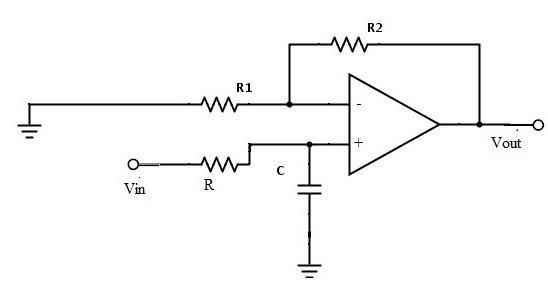
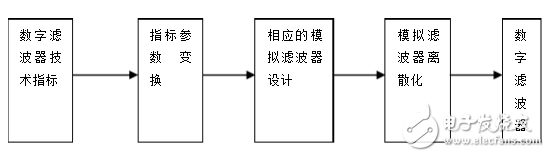
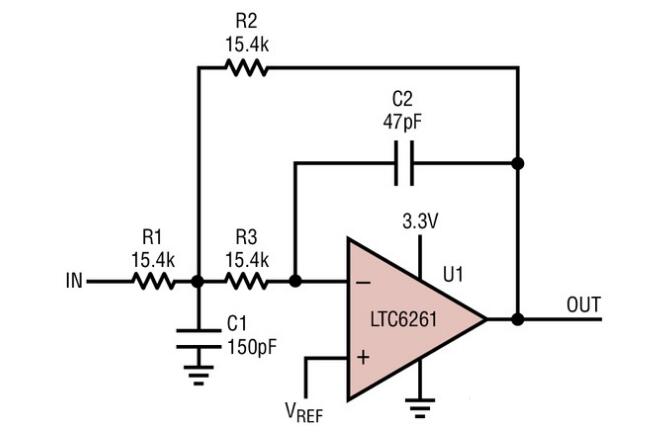
低通巴特沃斯數字濾波器的實例
一、Matlab計算濾波器系數
Matlab計算巴特沃斯低通濾波器系數過程如下:
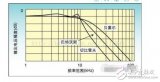
①根據給定的通帶截止頻率、通帶截止增益、阻帶截止頻率、阻帶截止增益,利用buttord函數計算巴特沃斯濾波器所需的最小階數和截止頻率。(由于要求中已給出截止頻率,故這步省去)
(圖是網上扒拉的,指標與本設計不符)
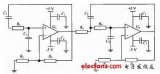
②根據上述計算得到的階數,利用buttap函數計算出巴特沃斯濾波器原型。
③利用lp2lp函數,將原型濾波器轉換成目標截止頻率的濾波器。
④利用脈沖響應不變法(impinvar函數)或是雙線性變換法(bilinear函數)將模擬濾波器轉換為數字濾波器。數字濾波器形式為z域有理函數,分子分母系數即為濾波器系數。
我這里選用的是脈沖響應不變法,因為計算得到的濾波器比較簡單,運算速度比較快。
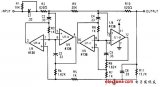
(從左到右:濾波器原型、模擬濾波器、數字濾波器)
設計過程matlab源碼如下:
Fs=15;%采樣頻率
Nn=12800;
N=2;%階數
Wc=1*2*pi;%截止頻率
[z,p,k]=buttap(N);%計算巴特沃斯濾波器原型
[Bap,Aap]=zp2tf(z,p,k);%轉換成多項式模式
[b,a]=lp2lp(Bap,Aap,Wc);%根據截止頻率計算模擬巴特沃斯濾波器系數
[bz,az]=impinvar(b,a,Fs);%用脈沖響應不變法離散化
figure(1)
[H,W]=freqz(bz,az,Nn,Fs);%繪制頻率特性曲線
subplot(2,1,1)
plot(W,20*log10(abs(H)));
gridon;
subplot(2,1,2)
plot(W,180/pi*unwrap(angle(H)));
gridon;
二、Matlab計算驗證
先在Matlab中驗證濾波函數。先編寫帶噪聲的輸入函數,然后經過濾波器函數后,觀察濾波效果。其中濾波器函數寫法為:
Filter函數為Matlab自帶函數,其算法為:
其中,a即為z域傳遞函數的分母系數,b為分子系數。例如本應用中:
則算法為az(1)*y(k)=bz(1)*x(k)+bz(2)*x(k-1)–az(2)*y(k-1)–az(3)*y(k-2)
Matlab中得到的結果如下(信號頻率0.1Hz,噪聲頻率6Hz):
三、C語言函數編寫與驗證
將上述算法翻譯成C語言,寫入單片機中。利用信號源輸出各種波形,單片機AD采樣進去之后,對采樣點進行濾波處理,將原始數據和濾波后的數據發送到上位機進行繪圖,得到圖像對比如下:
C函數源碼如下:
constfloatbz[2]={0,0.128580115806658};//分子
constfloataz[3]={1,-1.42252474659021,0.553007125840971};//分母
floatData_Output[DATA_LENTH];//輸出數據
float*but_filter(unsignedintlen,float*x)//len為輸入數據數組長度,x為輸入數據數組指針
{
unsignedinti=2;
staticfloatinit[2]={0,0};//初值,一開始設為0
if(len《2)//如果長度小于2,直接返回
returnData_Output;
Data_Output[0]=init[0];//賦初值
Data_Output[1]=init[1];
for(i=2;i《len;i++)
{
Data_Output[i]=bz[0]*x[i]+bz[1]*x[i-1]-az[1]*Data_Output[i-1]-az[2]*Data_Output[i-2];
/*算法為a1*y(k)=b1*x(k)+b2*x(k-1)-a(2)*y(k-1)-a(3)*y(k-2)*/
/*由于a1=1,故不做除法*/
}
init[0]=Data_Output[len-2];//考慮到會被連續調用,此次的終值作為下次的初值
init[1]=Data_Output[len-1];
returnData_Output;
}
 電子發燒友App
電子發燒友App









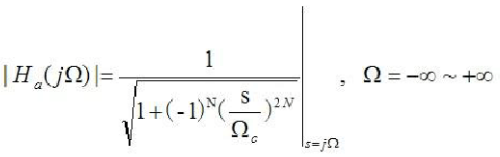












評論