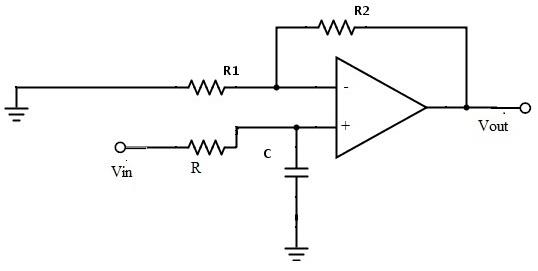
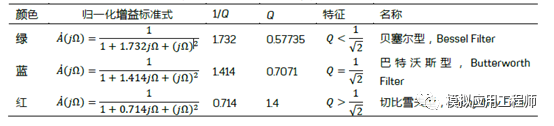
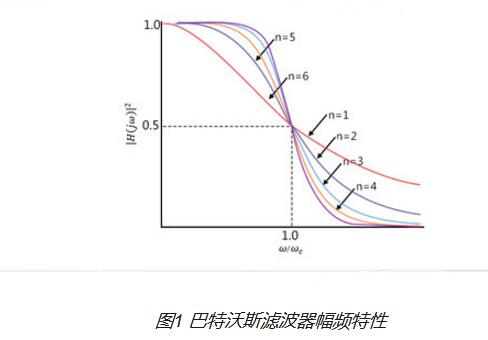
低通巴特沃斯數字濾波器的實例
一、Matlab計算濾波器系數
Matlab計算巴特沃斯低通濾波器系數過程如下:
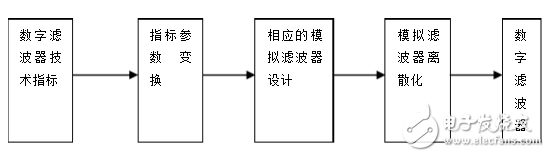
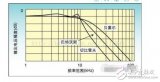
①根據給定的通帶截止頻率、通帶截止增益、阻帶截止頻率、阻帶截止增益,利用buttord函數計算巴特沃斯濾波器所需的最小階數和截止頻率。(由于要求中已給出截止頻率,故這步省去)
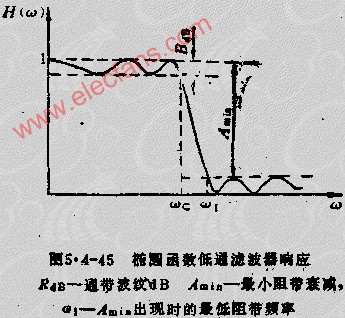
(圖是網上扒拉的,指標與本設計不符)
②根據上述計算得到的階數,利用buttap函數計算出巴特沃斯濾波器原型。
③利用lp2lp函數,將原型濾波器轉換成目標截止頻率的濾波器。
④利用脈沖響應不變法(impinvar函數)或是雙線性變換法(bilinear函數)將模擬濾波器轉換為數字濾波器。數字濾波器形式為z域有理函數,分子分母系數即為濾波器系數。
我這里選用的是脈沖響應不變法,因為計算得到的濾波器比較簡單,運算速度比較快。
(從左到右:濾波器原型、模擬濾波器、數字濾波器)
設計過程matlab源碼如下:
Fs=15;%采樣頻率
Nn=12800;
N=2;%階數
Wc=1*2*pi;%截止頻率
[z,p,k]=buttap(N);%計算巴特沃斯濾波器原型
[Bap,Aap]=zp2tf(z,p,k);%轉換成多項式模式
[b,a]=lp2lp(Bap,Aap,Wc);%根據截止頻率計算模擬巴特沃斯濾波器系數
[bz,az]=impinvar(b,a,Fs);%用脈沖響應不變法離散化
figure(1)
[H,W]=freqz(bz,az,Nn,Fs);%繪制頻率特性曲線
subplot(2,1,1)
plot(W,20*log10(abs(H)));
gridon;
subplot(2,1,2)
plot(W,180/pi*unwrap(angle(H)));
gridon;
二、Matlab計算驗證
先在Matlab中驗證濾波函數。先編寫帶噪聲的輸入函數,然后經過濾波器函數后,觀察濾波效果。其中濾波器函數寫法為:
Filter函數為Matlab自帶函數,其算法為:
其中,a即為z域傳遞函數的分母系數,b為分子系數。例如本應用中:
則算法為az(1)*y(k)=bz(1)*x(k)+bz(2)*x(k-1)–az(2)*y(k-1)–az(3)*y(k-2)
Matlab中得到的結果如下(信號頻率0.1Hz,噪聲頻率6Hz):
三、C語言函數編寫與驗證
將上述算法翻譯成C語言,寫入單片機中。利用信號源輸出各種波形,單片機AD采樣進去之后,對采樣點進行濾波處理,將原始數據和濾波后的數據發送到上位機進行繪圖,得到圖像對比如下:
C函數源碼如下:
constfloatbz[2]={0,0.128580115806658};//分子
constfloataz[3]={1,-1.42252474659021,0.553007125840971};//分母
floatData_Output[DATA_LENTH];//輸出數據
float*but_filter(unsignedintlen,float*x)//len為輸入數據數組長度,x為輸入數據數組指針
{
unsignedinti=2;
staticfloatinit[2]={0,0};//初值,一開始設為0
if(len《2)//如果長度小于2,直接返回
returnData_Output;
Data_Output[0]=init[0];//賦初值
Data_Output[1]=init[1];
for(i=2;i《len;i++)
{
Data_Output[i]=bz[0]*x[i]+bz[1]*x[i-1]-az[1]*Data_Output[i-1]-az[2]*Data_Output[i-2];
/*算法為a1*y(k)=b1*x(k)+b2*x(k-1)-a(2)*y(k-1)-a(3)*y(k-2)*/
/*由于a1=1,故不做除法*/
}
init[0]=Data_Output[len-2];//考慮到會被連續調用,此次的終值作為下次的初值
init[1]=Data_Output[len-1];
returnData_Output;
}
 電子發燒友App
電子發燒友App









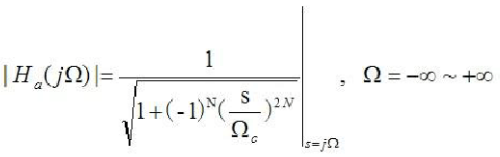












評論