哈夫曼樹的介紹
Huffman Tree,中文名是哈夫曼樹或霍夫曼樹,它是最優二叉樹。
定義:給定n個權值作為n個葉子結點,構造一棵二叉樹,若樹的帶權路徑長度達到最小,則這棵樹被稱為哈夫曼樹。 這個定義里面涉及到了幾個陌生的概念,下面就是一顆哈夫曼樹,我們來看圖解答。
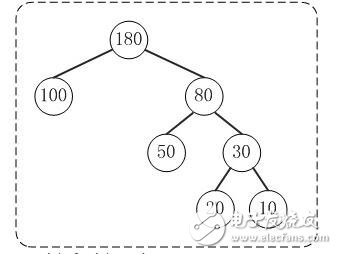
(1) 路徑和路徑長度
定義:在一棵樹中,從一個結點往下可以達到的孩子或孫子結點之間的通路,稱為路徑。通路中分支的數目稱為路徑長度。若規定根結點的層數為1,則從根結點到第L層結點的路徑長度為L-1。
例子:100和80的路徑長度是1,50和30的路徑長度是2,20和10的路徑長度是3。
(2) 結點的權及帶權路徑長度
定義:若將樹中結點賦給一個有著某種含義的數值,則這個數值稱為該結點的權。結點的帶權路徑長度為:從根結點到該結點之間的路徑長度與該結點的權的乘積。
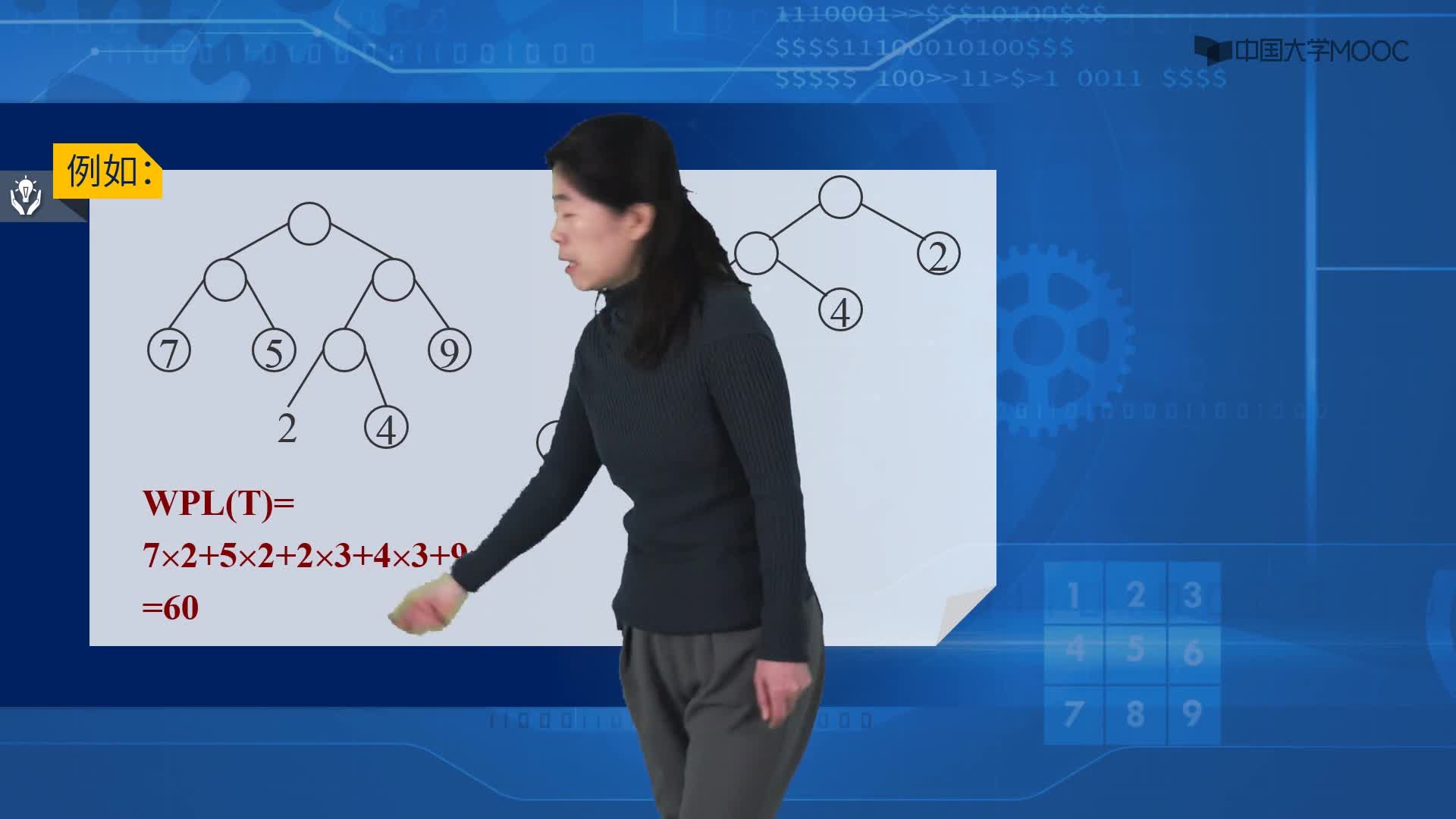
例子:節點20的路徑長度是3,它的帶權路徑長度= 路徑長度 * 權 = 3 * 20 = 60。
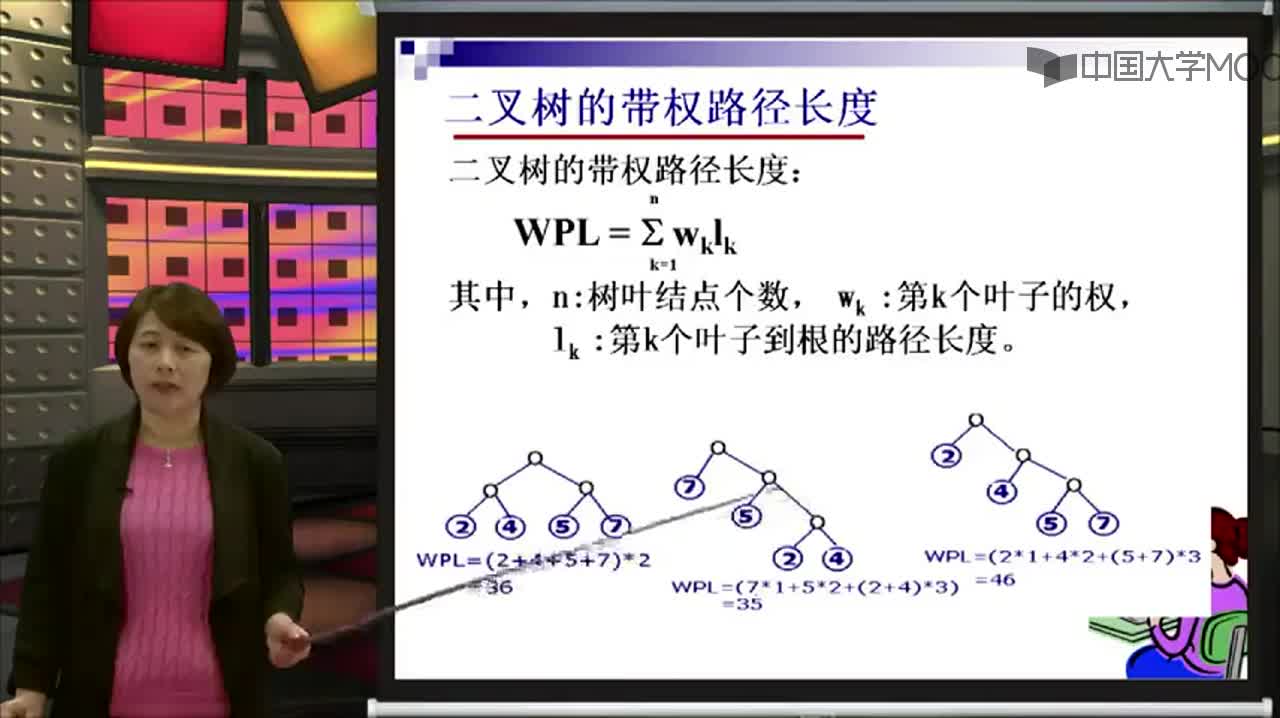
(3) 樹的帶權路徑長度
定義:樹的帶權路徑長度規定為所有葉子結點的帶權路徑長度之和,記為WPL。
例子:示例中,樹的WPL= 1*100 + 2*50 + 3*20 + 3*10 = 100 + 100 + 60 + 30 = 290。
比較下面兩棵樹
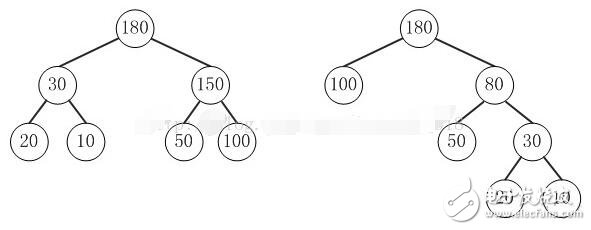
上面的兩棵樹都是以{10, 20, 50, 100}為葉子節點的樹。
左邊的樹WPL=2*10 + 2*20 + 2*50 + 2*100 = 360
右邊的樹WPL=290
左邊的樹WPL 》 右邊的樹的WPL。你也可以計算除上面兩種示例之外的情況,但實際上右邊的樹就是{10,20,50,100}對應的哈夫曼樹。至此,應該對哈夫曼樹的概念有了一定的了解了,下面看看如何去構造一棵哈夫曼樹。
 電子發燒友App
電子發燒友App


































































評論