哈夫曼樹的圖文解析

　　假設有n個權值，則構造出的哈夫曼樹有n個葉子結點。 n個權值分別設為 w1、w2、…、wn，哈夫曼樹的構造規則為：

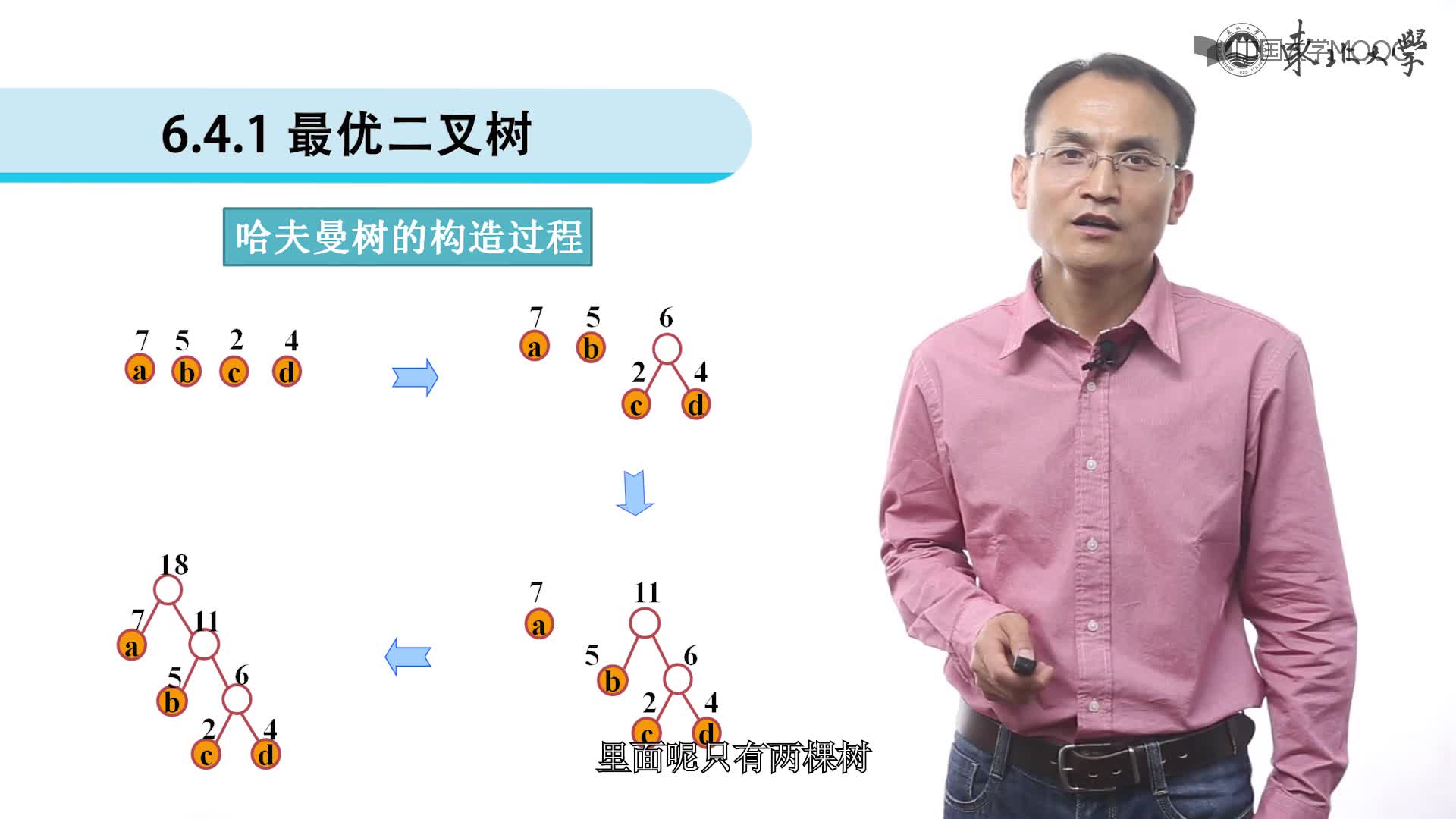
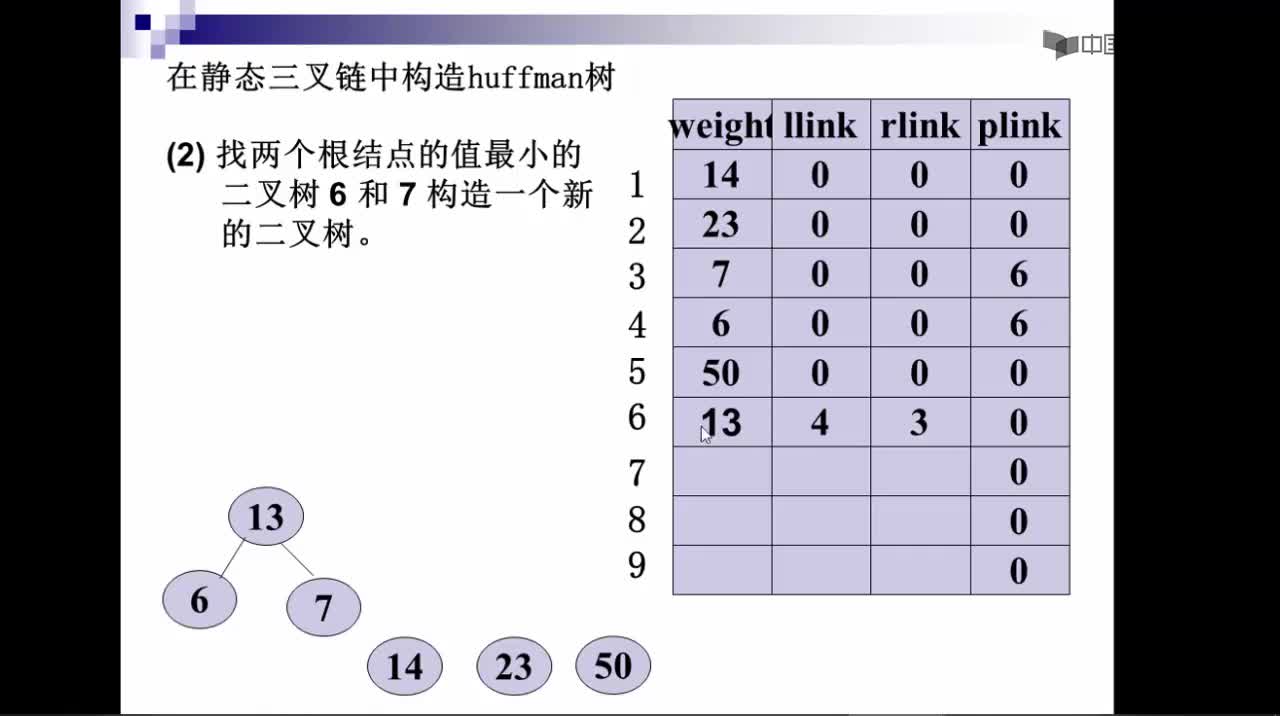
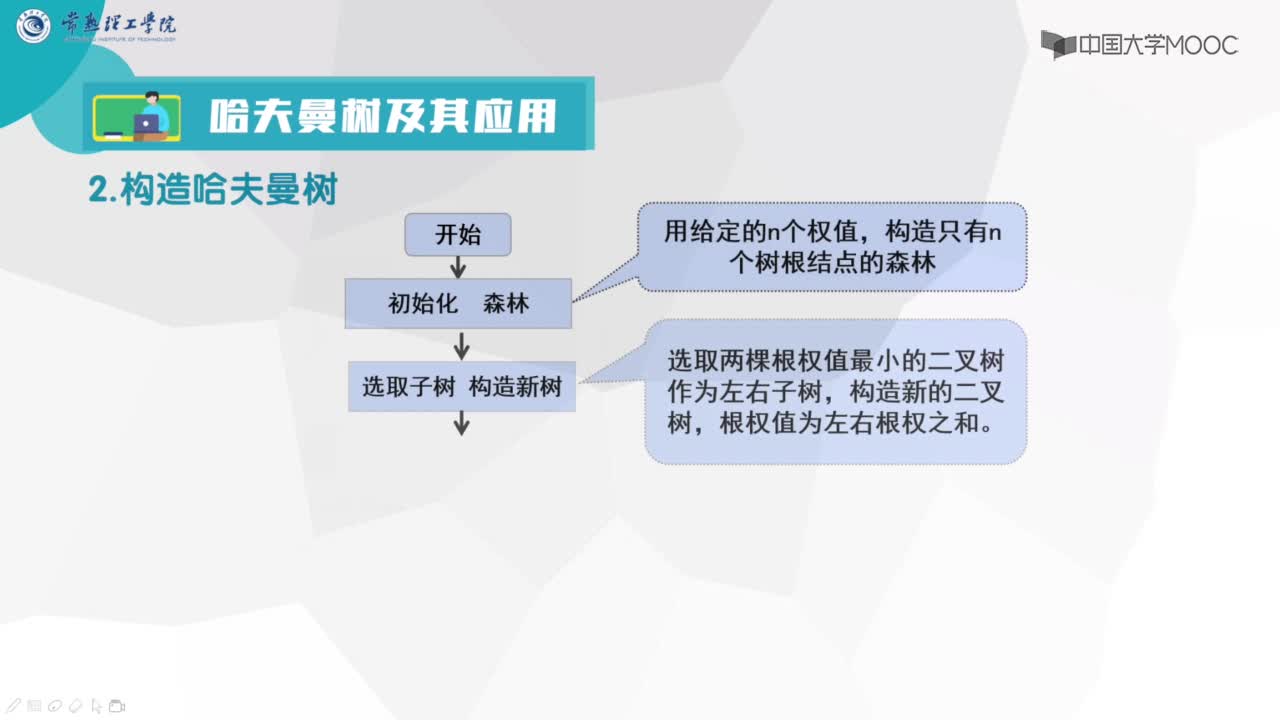
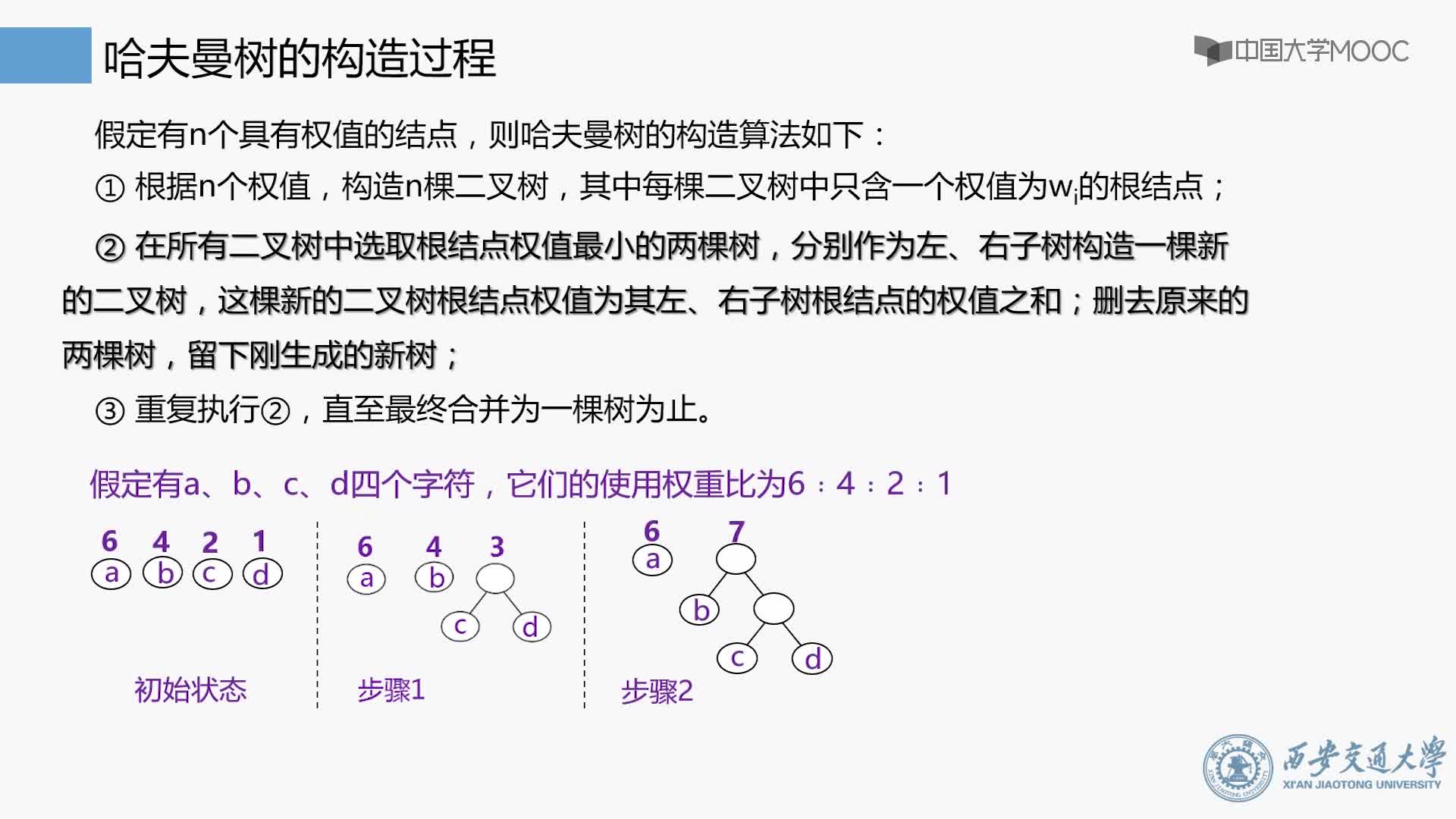
　　1. 將w1、w2、…，wn看成是有n 棵樹的森林（每棵樹僅有一個結點）；

　　2. 在森林中選出根結點的權值最小的兩棵樹進行合并，作為一棵新樹的左、右子樹，且新樹的根結點權值為其左、右子樹根結點權值之和；

　　3. 從森林中刪除選取的兩棵樹，并將新樹加入森林；

　　4. 重復（02）、（03）步，直到森林中只剩一棵樹為止，該樹即為所求得的哈夫曼樹。

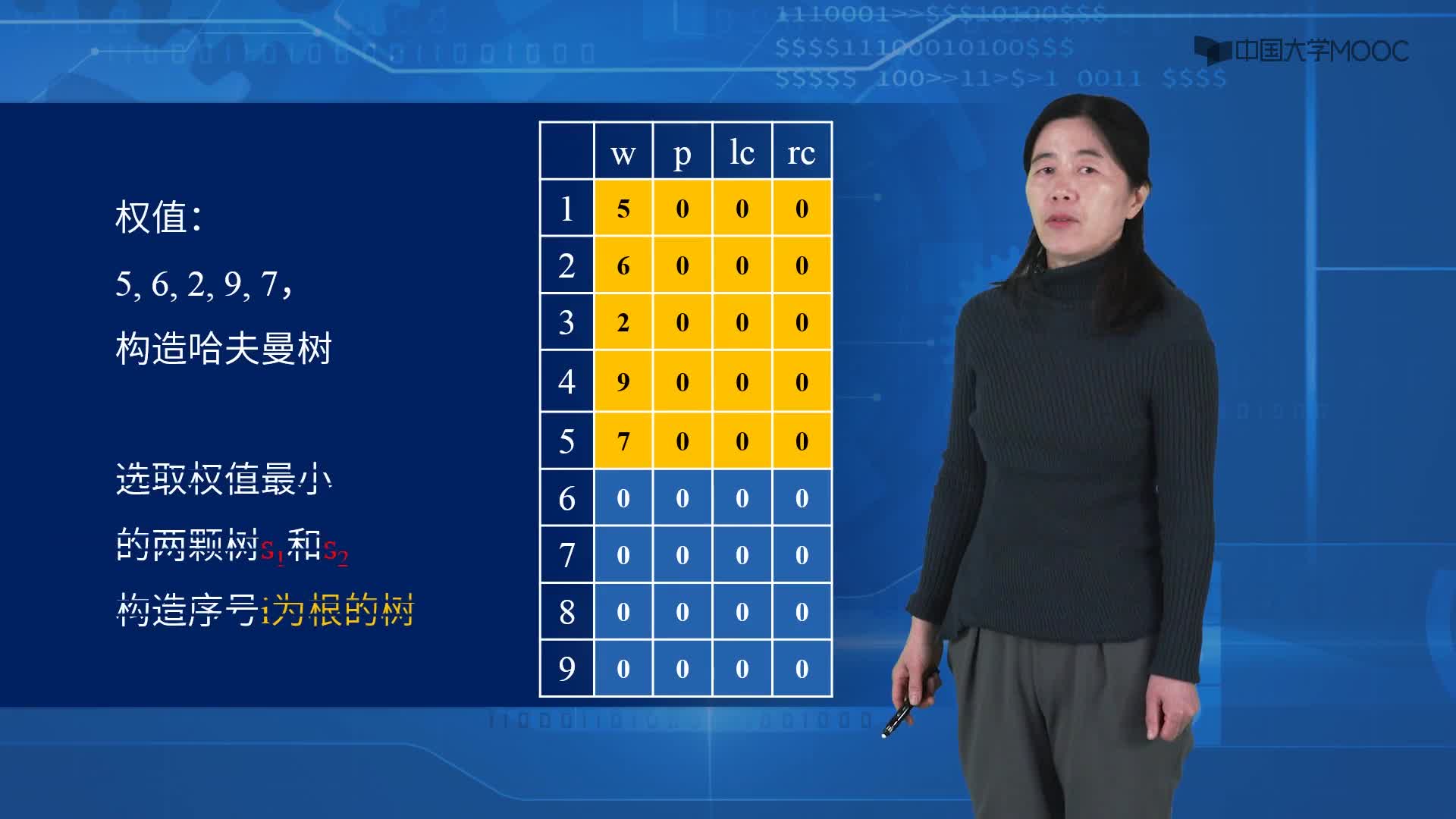
　　以{5，6，7，8，15}為例，來構造一棵哈夫曼樹。

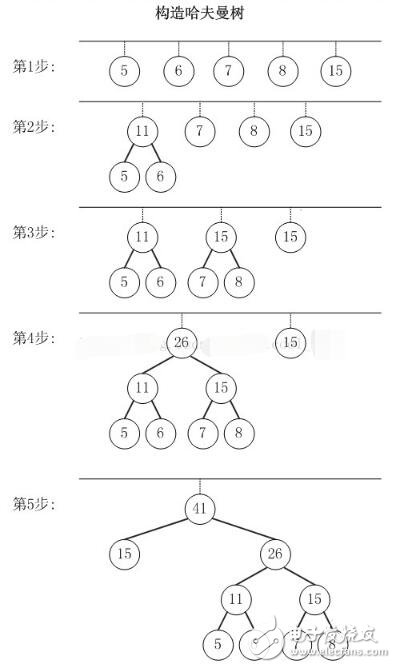
　　第1步：創建森林，森林包括5棵樹，這5棵樹的權值分別是5，6，7，8，15。

　　第2步：在森林中，選擇根節點權值最小的兩棵樹（5和6）來進行合并，將它們作為一顆新樹的左右孩子（誰左誰右無關緊要，這里，我們選擇較小的作為左孩子），并且新樹的權值是左右孩子的權值之和。即，新樹的權值是11。 然后，將“樹5”和“樹6”從森林中刪除，并將新的樹（樹11）添加到森林中。

　　第3步：在森林中，選擇根節點權值最小的兩棵樹（7和8）來進行合并。得到的新樹的權值是15。 然后，將“樹7”和“樹8”從森林中刪除，并將新的樹（樹15）添加到森林中。

　　第4步：在森林中，選擇根節點權值最小的兩棵樹（11和15）來進行合并。得到的新樹的權值是26。 然后，將“樹11”和“樹15”從森林中刪除，并將新的樹（樹26）添加到森林中。

　　第5步：在森林中，選擇根節點權值最小的兩棵樹（15和26）來進行合并。得到的新樹的權值是41。 然后，將“樹15”和“樹26”從森林中刪除，并將新的樹（樹41）添加到森林中。

　　此時，森林中只有一棵樹（樹41）。這棵樹就是我們需要的哈夫曼樹！

　　哈夫曼樹是一種樹形結構，用哈夫曼樹的方法解編程題的算法就叫做哈夫曼算法。樹并不是指植物，而是一種數據結構，因為其存放方式頗有點象一棵樹有樹叉因而稱為樹。 最簡哈夫曼樹是由德國數學家馮。哈夫曼 發現的，此樹的特點就是引出的路程最短。

　　哈夫曼算法

　　哈夫曼樹是一種樹形結構，用哈夫曼樹的方法解編程題的算法就叫做哈夫曼算法。樹并不是指植物，而是一種數據結構。

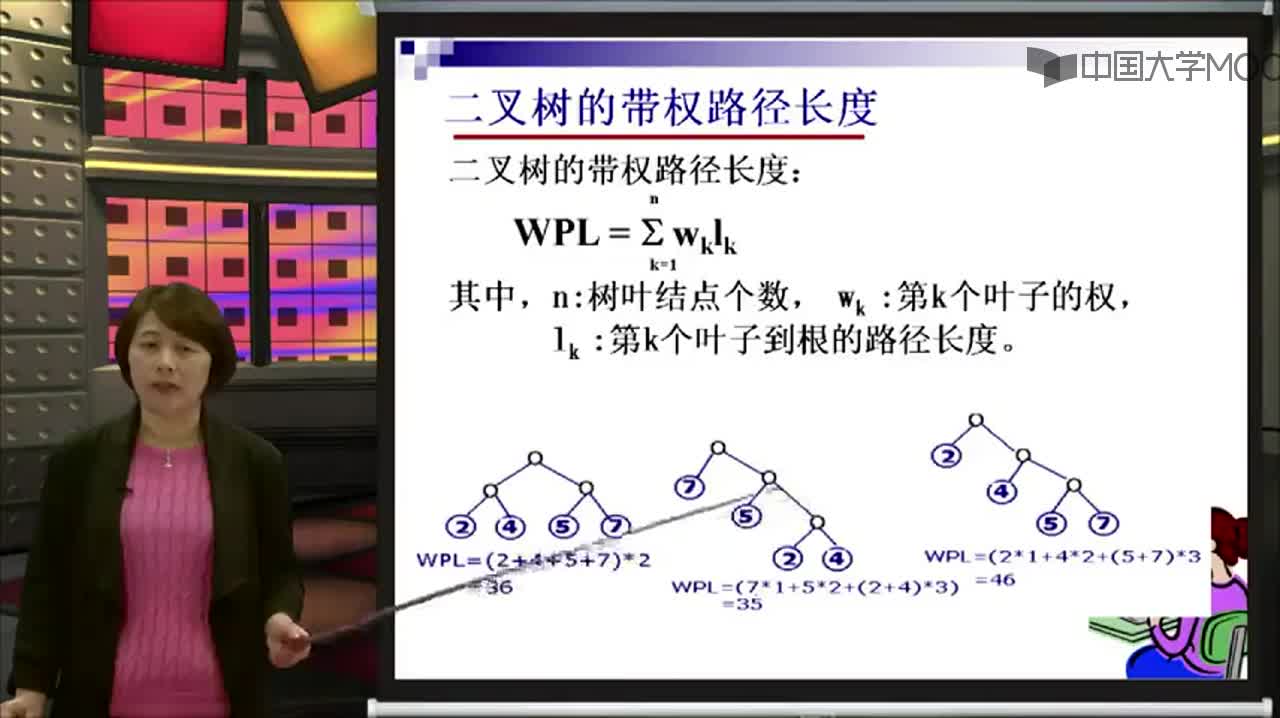
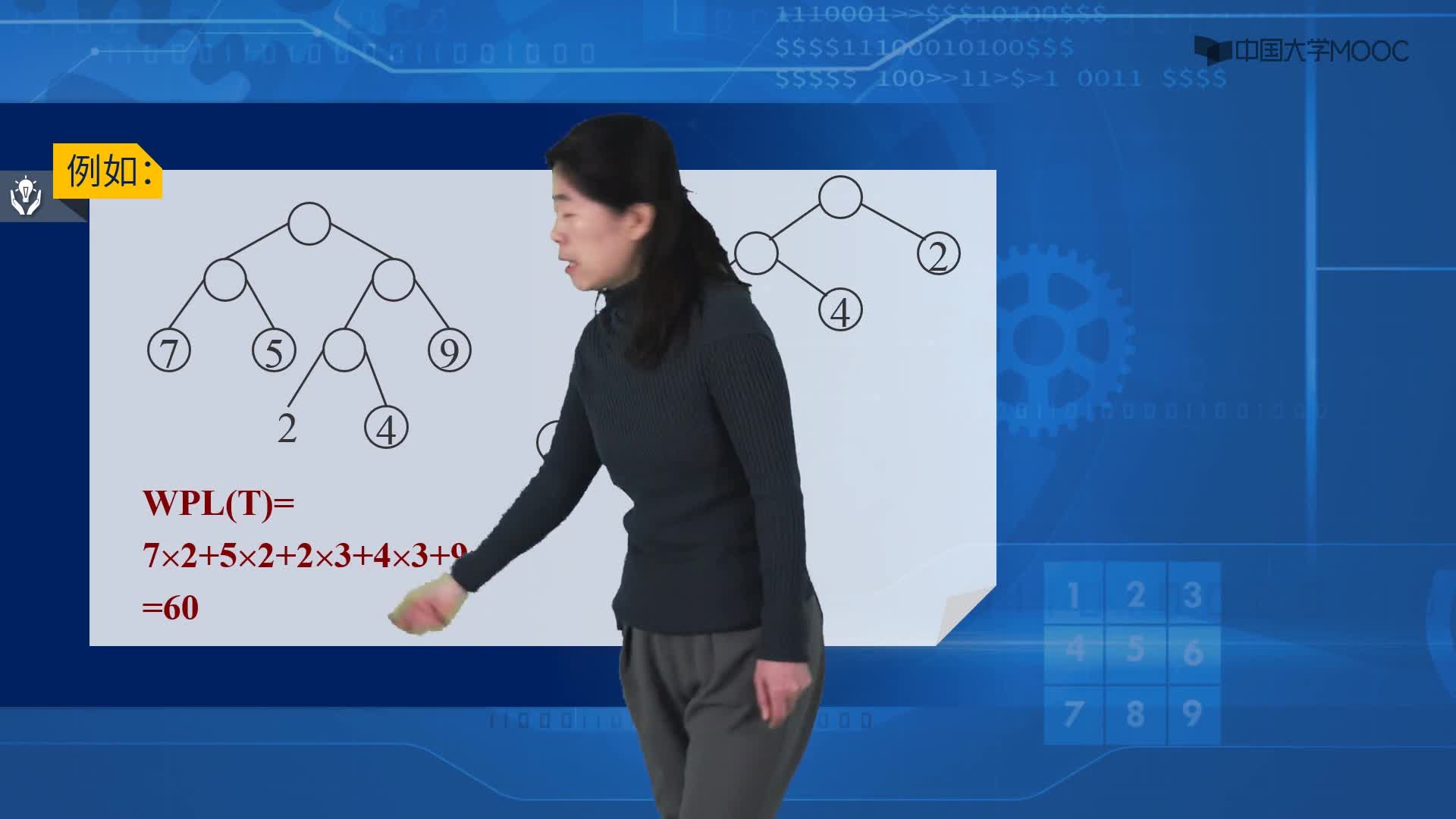
　　定義：它是由n個帶權葉子結點構成的所有二叉樹中帶權路徑長度最短的二叉樹。因為這種樹最早由哈夫曼（Huffman）研究，所以稱為哈夫曼樹，又叫最優二叉樹。

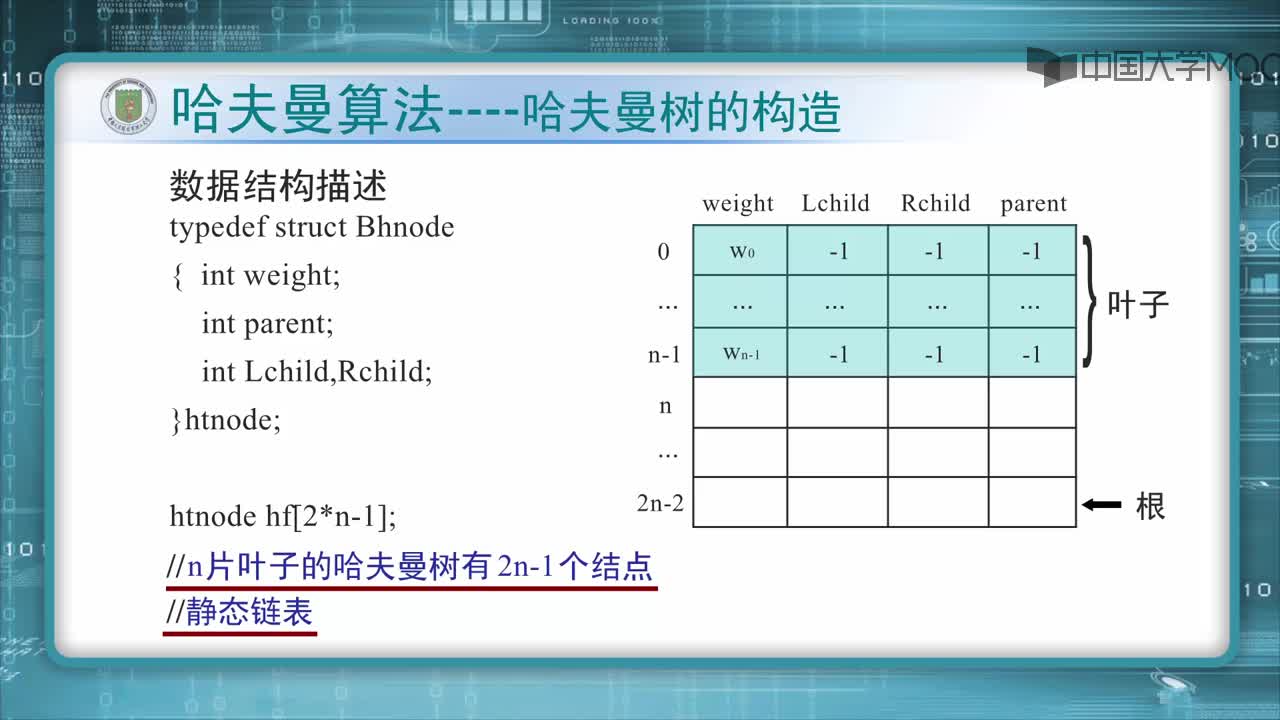
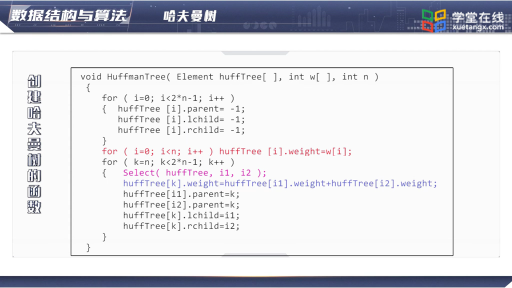
　　構造哈夫曼樹

　　［html］ view plain copy/*

　　* 創建Huffman樹

　　*

　　* @param 權值數組

　　*/

　　public Huffman（int a［］） {

　　HuffmanNode parent = null;

　　MinHeap heap;

　　// 建立數組a對應的最小堆

　　heap = new MinHeap（a）;

　　for（int i=0; i《a.length-1; i++） {

　　HuffmanNode left = heap.dumpFromMinimum（）; // 最小節點是左孩子

　　HuffmanNode right = heap.dumpFromMinimum（）; // 其次才是右孩子

　　// 新建parent節點，左右孩子分別是left/right；

　　// parent的大小是左右孩子之和

　　parent = new HuffmanNode（left.key+right.key， left， right， null）;

　　left.parent = parent;

　　right.parent = parent;

　　// 將parent節點數據拷貝到“最小堆”中

　　heap.insert（parent）;

　　}

　　mRoot = parent;

　　// 銷毀最小堆

　　heap.destroy（）;

　　}

　　首先創建最小堆，然后進入for循環。

　　每次循環時：

　　（1） 首先，將最小堆中的最小節點拷貝一份并賦值給left，然后重塑最小堆（將最小節點和后面的節點交換位置，接著將“交換位置后的最小節點”之前的全部元素重新構造成最小堆）；

　　（2） 接著，再將最小堆中的最小節點拷貝一份并將其賦值right，然后再次重塑最小堆；

　　（3） 然后，新建節點parent，并將它作為left和right的父節點；

　　（4） 接著，將parent的數據復制給最小堆中的指定節點。