哈夫曼樹的介紹
Huffman Tree,中文名是哈夫曼樹或霍夫曼樹,它是最優二叉樹。
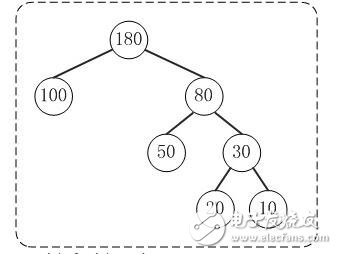
定義:給定n個權值作為n個葉子結點,構造一棵二叉樹,若樹的帶權路徑長度達到最小,則這棵樹被稱為哈夫曼樹。 這個定義里面涉及到了幾個陌生的概念,下面就是一顆哈夫曼樹,我們來看圖解答。
(1) 路徑和路徑長度
定義:在一棵樹中,從一個結點往下可以達到的孩子或孫子結點之間的通路,稱為路徑。通路中分支的數目稱為路徑長度。若規定根結點的層數為1,則從根結點到第L層結點的路徑長度為L-1。
例子:100和80的路徑長度是1,50和30的路徑長度是2,20和10的路徑長度是3。
(2) 結點的權及帶權路徑長度
定義:若將樹中結點賦給一個有著某種含義的數值,則這個數值稱為該結點的權。結點的帶權路徑長度為:從根結點到該結點之間的路徑長度與該結點的權的乘積。
例子:節點20的路徑長度是3,它的帶權路徑長度= 路徑長度 * 權 = 3 * 20 = 60。
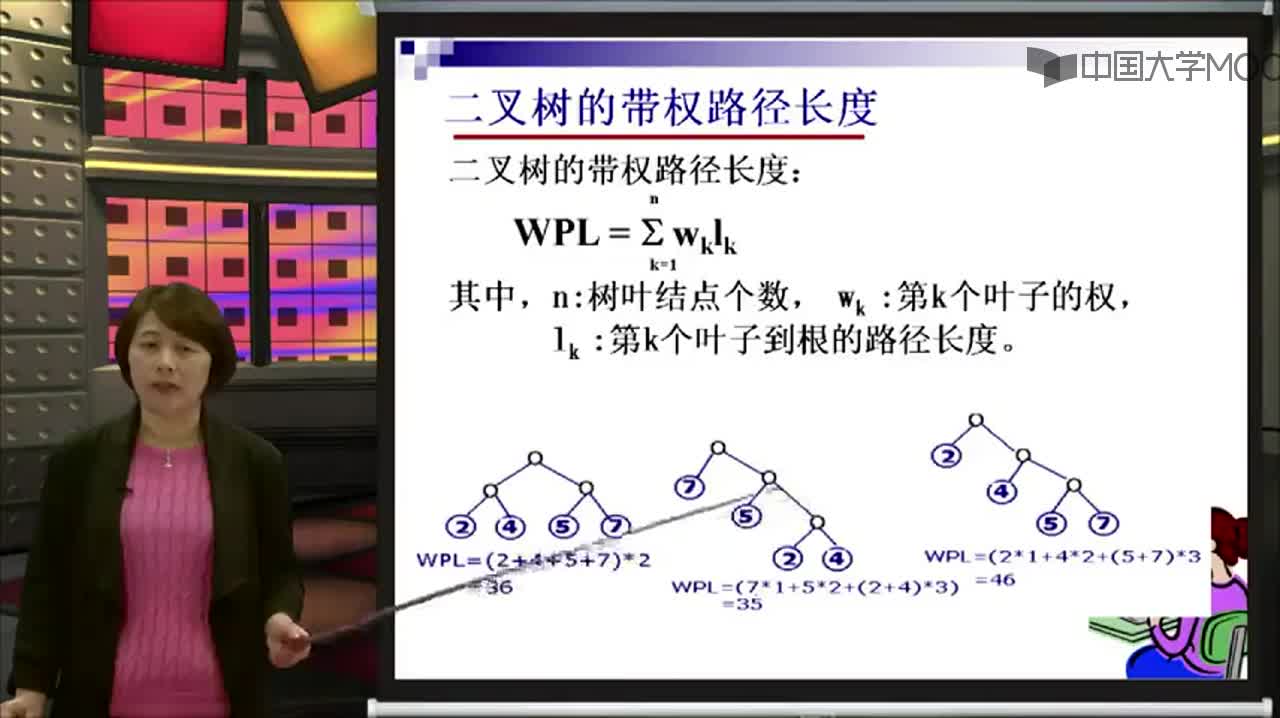
(3) 樹的帶權路徑長度
定義:樹的帶權路徑長度規定為所有葉子結點的帶權路徑長度之和,記為WPL。
例子:示例中,樹的WPL= 1*100 + 2*50 + 3*20 + 3*10 = 100 + 100 + 60 + 30 = 290。
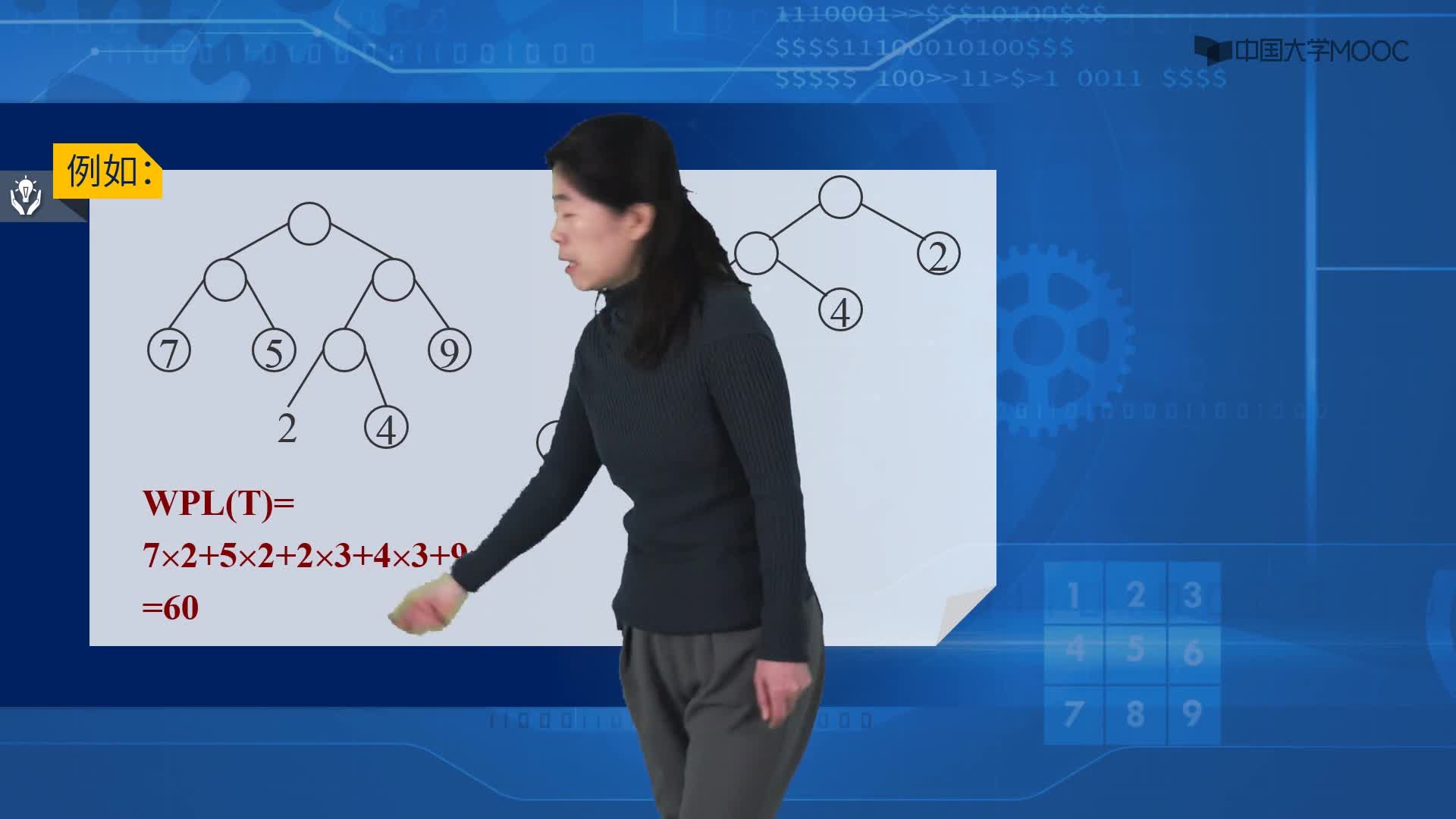
比較下面兩棵樹
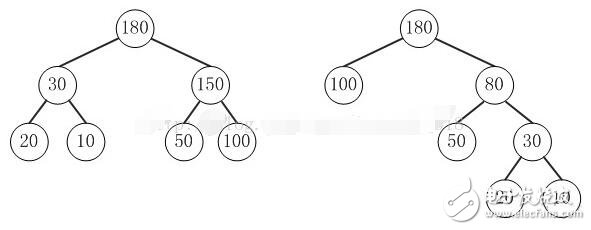
上面的兩棵樹都是以{10, 20, 50, 100}為葉子節點的樹。
左邊的樹WPL=2*10 + 2*20 + 2*50 + 2*100 = 360
右邊的樹WPL=290
左邊的樹WPL 》 右邊的樹的WPL。你也可以計算除上面兩種示例之外的情況,但實際上右邊的樹就是{10,20,50,100}對應的哈夫曼樹。至此,應該對哈夫曼樹的概念有了一定的了解了,下面看看如何去構造一棵哈夫曼樹。
哈夫曼樹的圖文解析
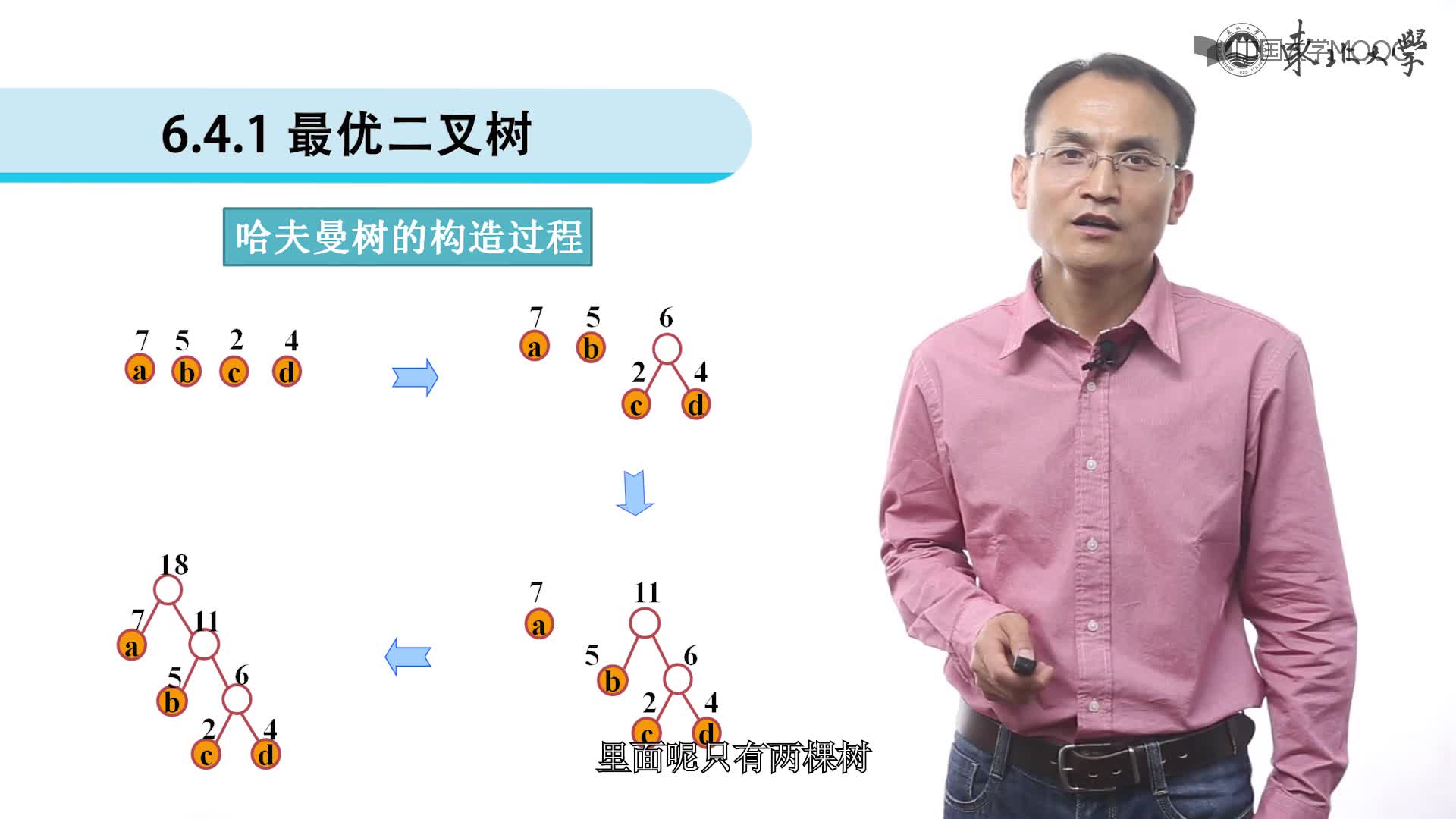
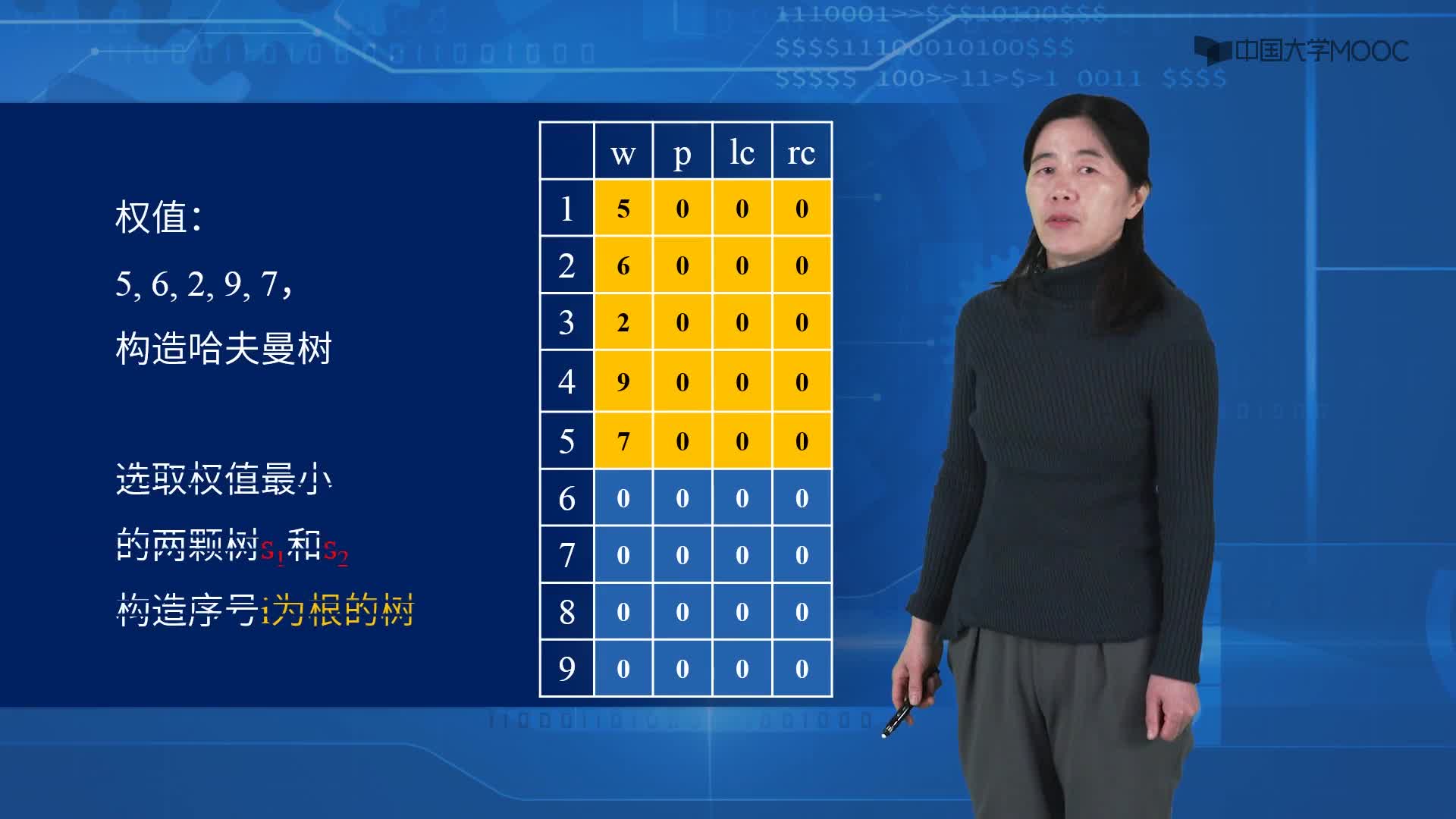
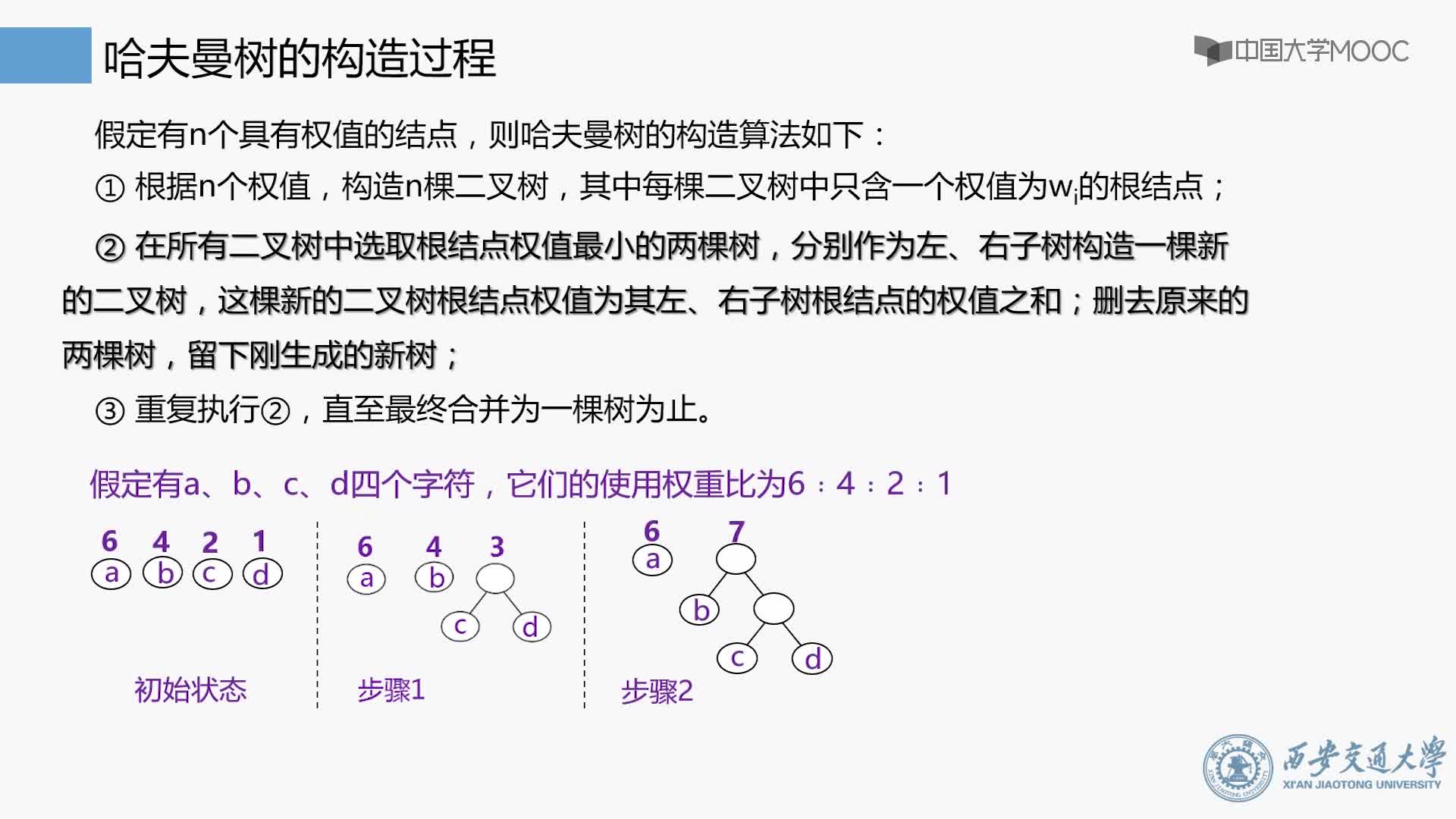
假設有n個權值,則構造出的哈夫曼樹有n個葉子結點。 n個權值分別設為 w1、w2、…、wn,哈夫曼樹的構造規則為:
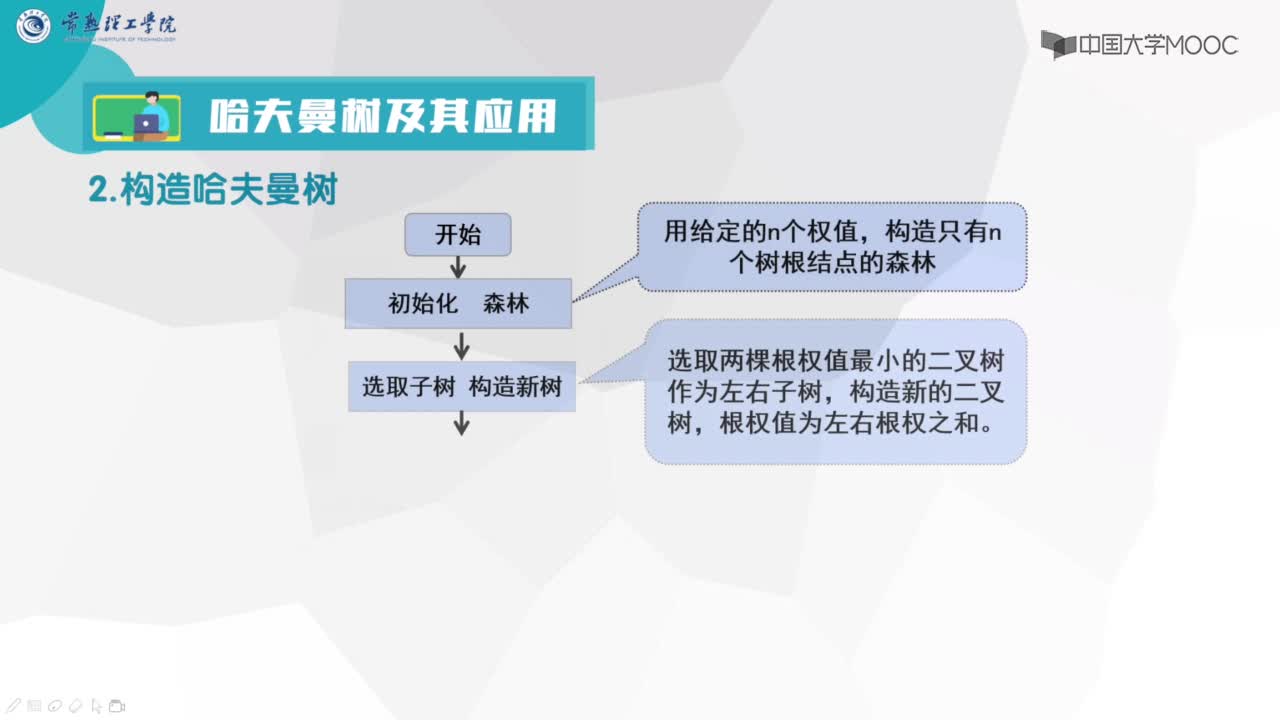
1. 將w1、w2、…,wn看成是有n 棵樹的森林(每棵樹僅有一個結點);
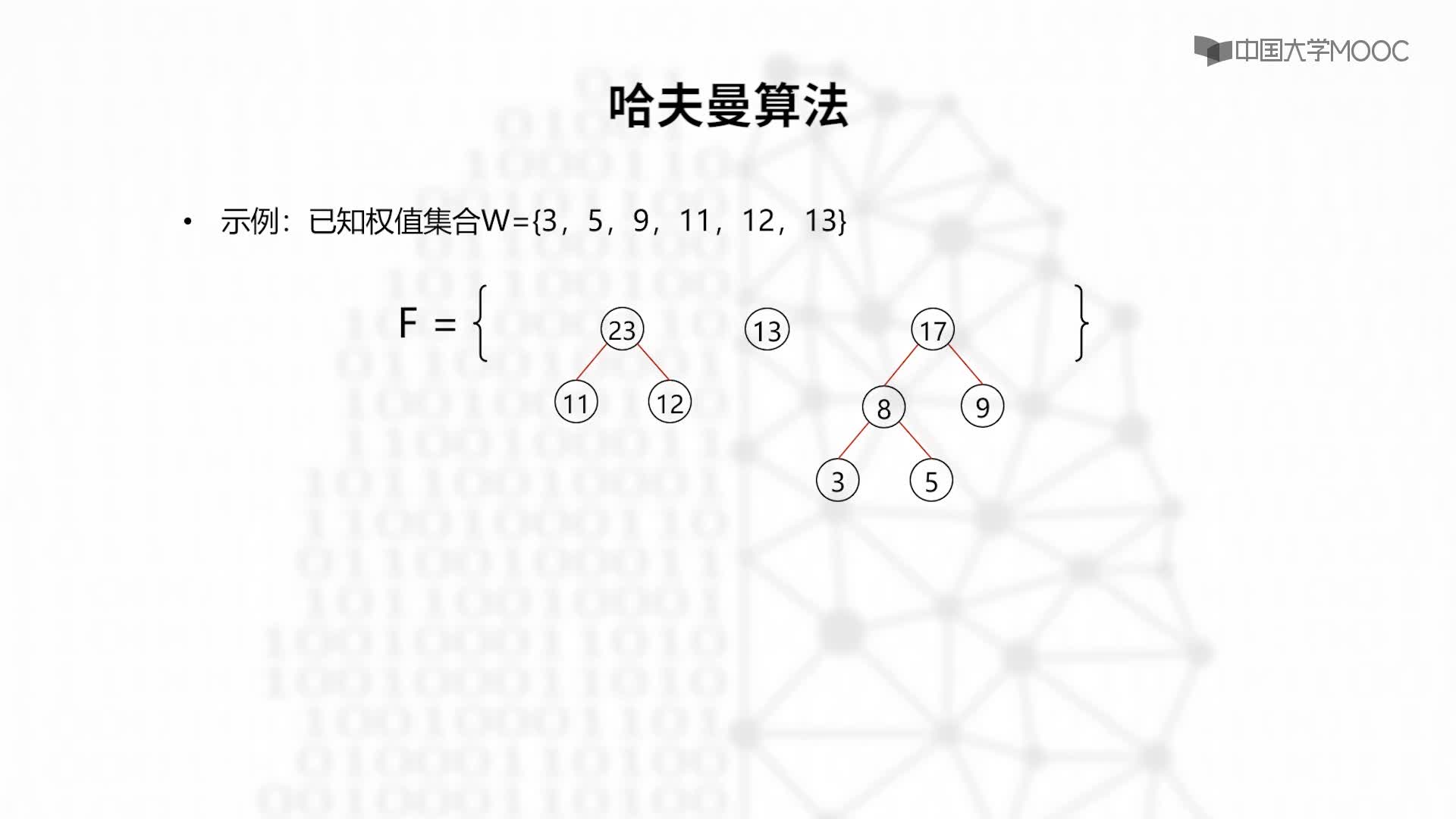
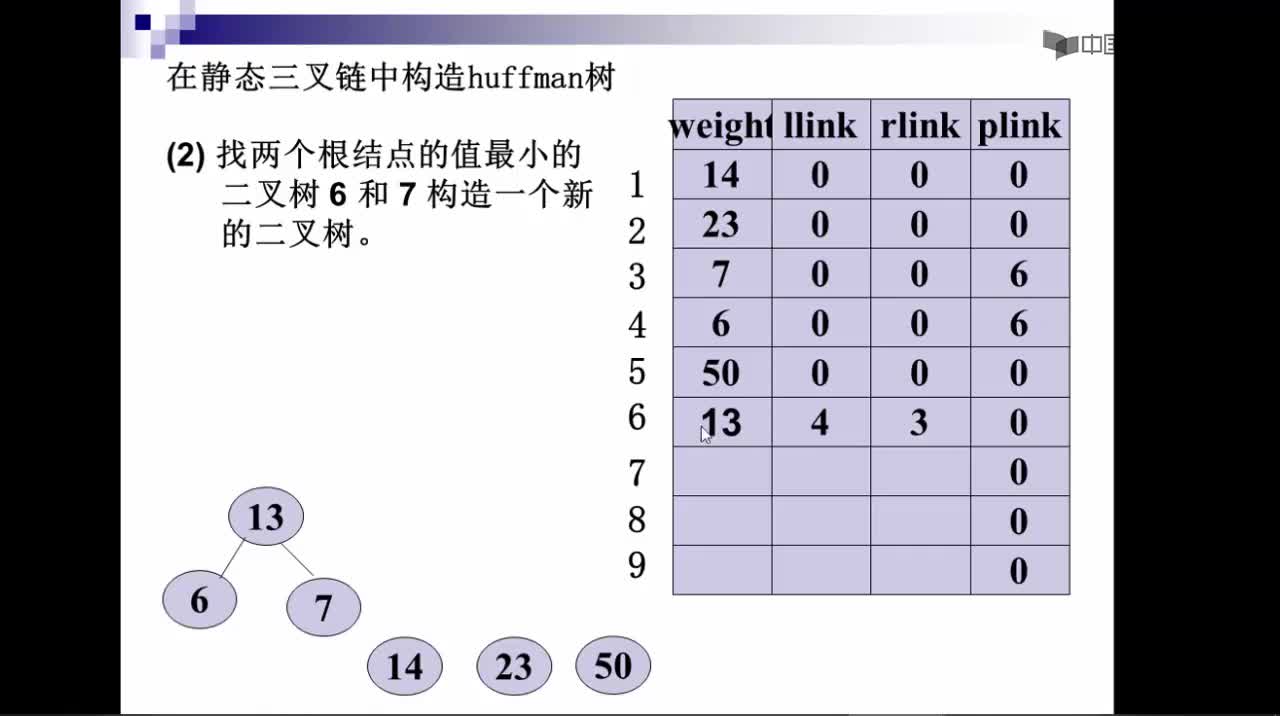
2. 在森林中選出根結點的權值最小的兩棵樹進行合并,作為一棵新樹的左、右子樹,且新樹的根結點權值為其左、右子樹根結點權值之和;
3. 從森林中刪除選取的兩棵樹,并將新樹加入森林;
4. 重復(02)、(03)步,直到森林中只剩一棵樹為止,該樹即為所求得的哈夫曼樹。
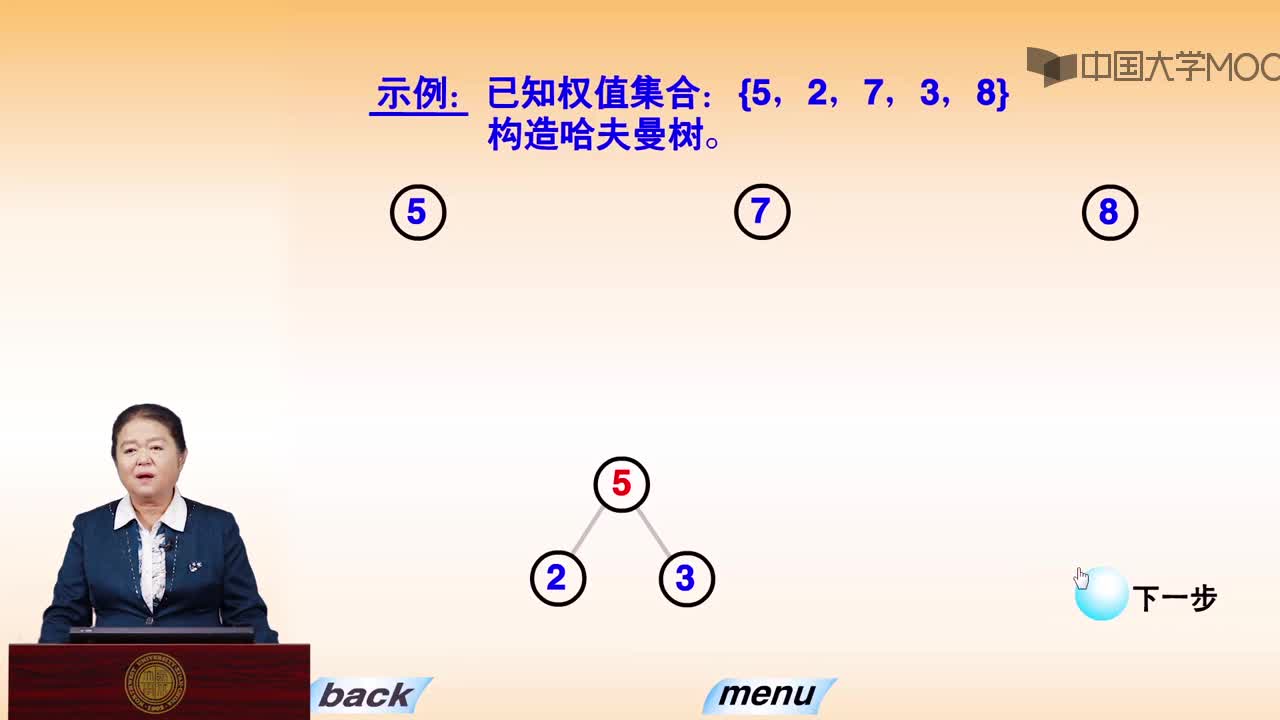
以{5,6,7,8,15}為例,來構造一棵哈夫曼樹。
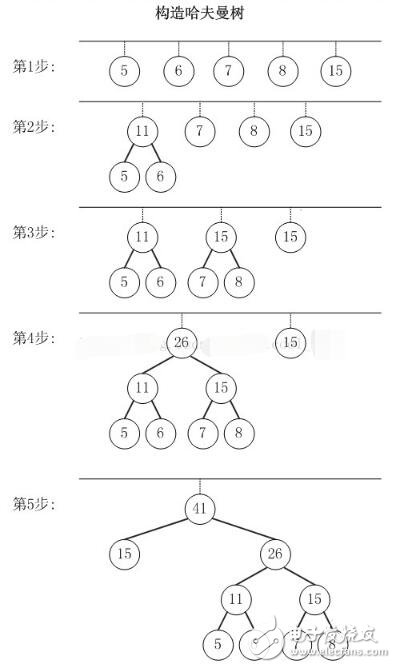
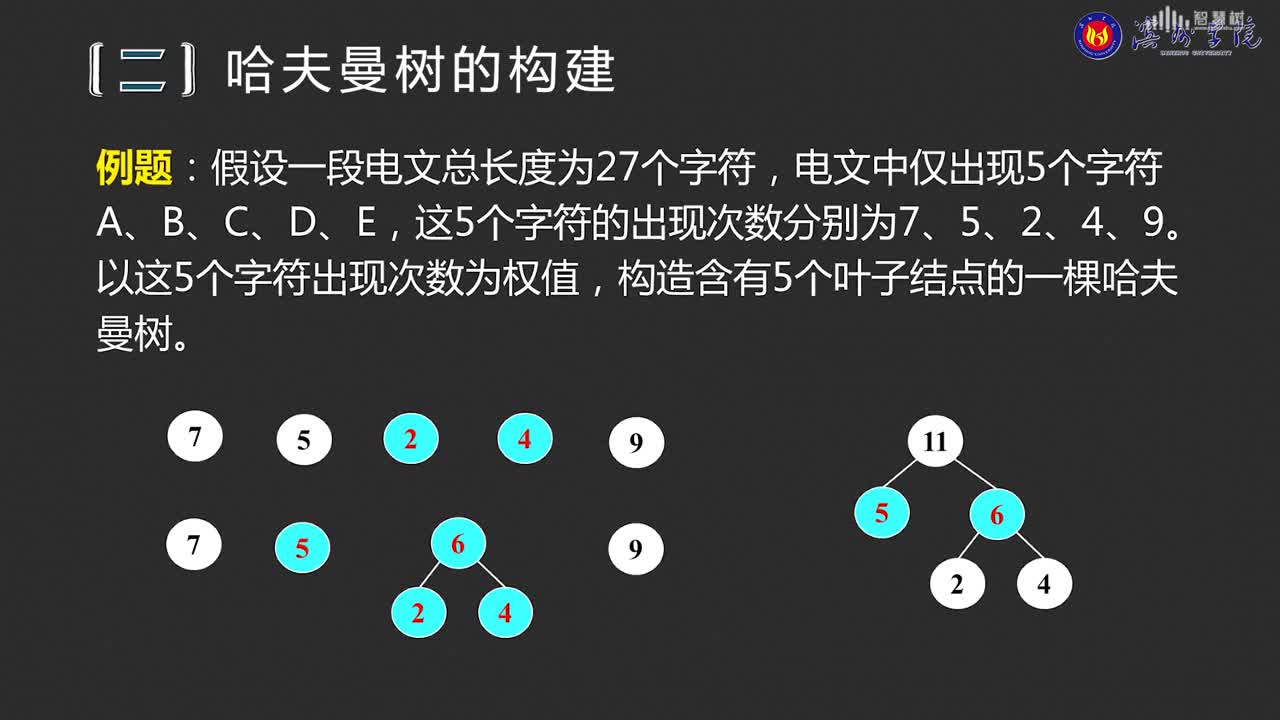
第1步:創建森林,森林包括5棵樹,這5棵樹的權值分別是5,6,7,8,15。
第2步:在森林中,選擇根節點權值最小的兩棵樹(5和6)來進行合并,將它們作為一顆新樹的左右孩子(誰左誰右無關緊要,這里,我們選擇較小的作為左孩子),并且新樹的權值是左右孩子的權值之和。即,新樹的權值是11。 然后,將“樹5”和“樹6”從森林中刪除,并將新的樹(樹11)添加到森林中。
第3步:在森林中,選擇根節點權值最小的兩棵樹(7和8)來進行合并。得到的新樹的權值是15。 然后,將“樹7”和“樹8”從森林中刪除,并將新的樹(樹15)添加到森林中。
第4步:在森林中,選擇根節點權值最小的兩棵樹(11和15)來進行合并。得到的新樹的權值是26。 然后,將“樹11”和“樹15”從森林中刪除,并將新的樹(樹26)添加到森林中。
第5步:在森林中,選擇根節點權值最小的兩棵樹(15和26)來進行合并。得到的新樹的權值是41。 然后,將“樹15”和“樹26”從森林中刪除,并將新的樹(樹41)添加到森林中。
此時,森林中只有一棵樹(樹41)。這棵樹就是我們需要的哈夫曼樹!
哈夫曼樹是一種樹形結構,用哈夫曼樹的方法解編程題的算法就叫做哈夫曼算法。樹并不是指植物,而是一種數據結構,因為其存放方式頗有點象一棵樹有樹叉因而稱為樹。 最簡哈夫曼樹是由德國數學家馮。哈夫曼 發現的,此樹的特點就是引出的路程最短。
哈夫曼算法
哈夫曼樹是一種樹形結構,用哈夫曼樹的方法解編程題的算法就叫做哈夫曼算法。樹并不是指植物,而是一種數據結構。
定義:它是由n個帶權葉子結點構成的所有二叉樹中帶權路徑長度最短的二叉樹。因為這種樹最早由哈夫曼(Huffman)研究,所以稱為哈夫曼樹,又叫最優二叉樹。
構造哈夫曼樹
[html] view plain copy/*
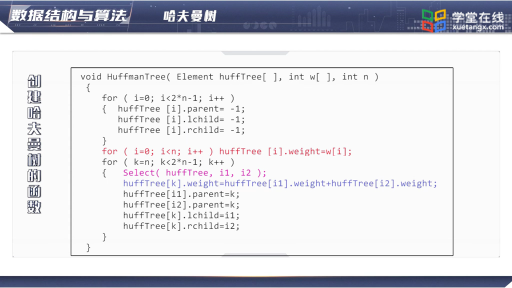
* 創建Huffman樹
*
* @param 權值數組
*/
public Huffman(int a[]) {
HuffmanNode parent = null;
MinHeap heap;
// 建立數組a對應的最小堆
heap = new MinHeap(a);
for(int i=0; i《a.length-1; i++) {
HuffmanNode left = heap.dumpFromMinimum(); // 最小節點是左孩子
HuffmanNode right = heap.dumpFromMinimum(); // 其次才是右孩子
// 新建parent節點,左右孩子分別是left/right;
// parent的大小是左右孩子之和
parent = new HuffmanNode(left.key+right.key, left, right, null);
left.parent = parent;
right.parent = parent;
// 將parent節點數據拷貝到“最小堆”中
heap.insert(parent);
}
mRoot = parent;
// 銷毀最小堆
heap.destroy();
}
首先創建最小堆,然后進入for循環。
每次循環時:
(1) 首先,將最小堆中的最小節點拷貝一份并賦值給left,然后重塑最小堆(將最小節點和后面的節點交換位置,接著將“交換位置后的最小節點”之前的全部元素重新構造成最小堆);
(2) 接著,再將最小堆中的最小節點拷貝一份并將其賦值right,然后再次重塑最小堆;
(3) 然后,新建節點parent,并將它作為left和right的父節點;
(4) 接著,將parent的數據復制給最小堆中的指定節點。
哈夫曼算法原理
1952年, David A. Huffman提出了一個不同的算法,這個算法可以為任何的可能性提供出一個理想的樹。香農-范諾編碼(Shanno-Fano)是從樹的根節點到葉子節點所進行的的編碼,哈夫曼編碼算法卻是從相反的方向,暨從葉子節點到根節點的方向編碼的。
1.為每個符號建立一個葉子節點,并加上其相應的發生頻率
2.當有一個以上的節點存在時,進行下列循環:
1)把這些節點作為帶權值的二叉樹的根節點,左右子樹為空
2)選擇兩棵根結點權值最小的樹作為左右子樹構造一棵新的二叉樹,且至新的二叉樹的根結點的權值為其左右子樹上根結點的權值之和。
3)把權值最小的兩個根節點移除
4)將新的二叉樹加入隊列中。
5)最后剩下的節點暨為根節點,此時二叉樹已經完成。
哈夫曼樹的應用
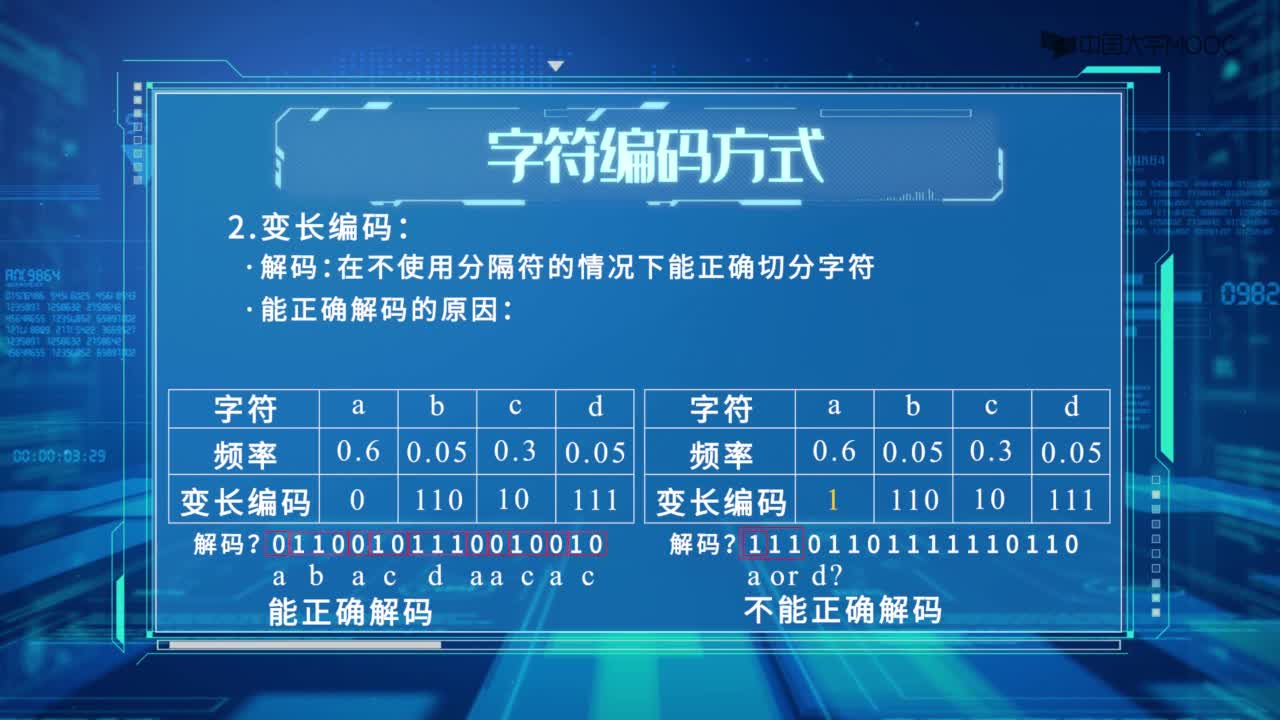
哈夫曼編碼:
哈夫曼樹可以直接應用于通信及數據傳送中的二進制編碼。設: D={d1,d2,d3…dn}為需要編碼的字符集合。
W={w1,w2,w3,…wn}為D中各字符出現的頻率。 現要對D中的字符進行二進制編碼,使得:
(1) 按給出的編碼傳輸文件時,通信編碼的總長最短。
(2) 若di不等于dj,則di的編碼不可能是dj的編碼的開始部分(前綴)。
滿足上述要求的二進制編碼稱為最優前綴編碼。 上述要求的第一條是為了提高傳輸的速度,第二條是為了保證傳輸的信息在譯碼時無二性,所以在字符的編碼中間不需要添加任意的分割符。
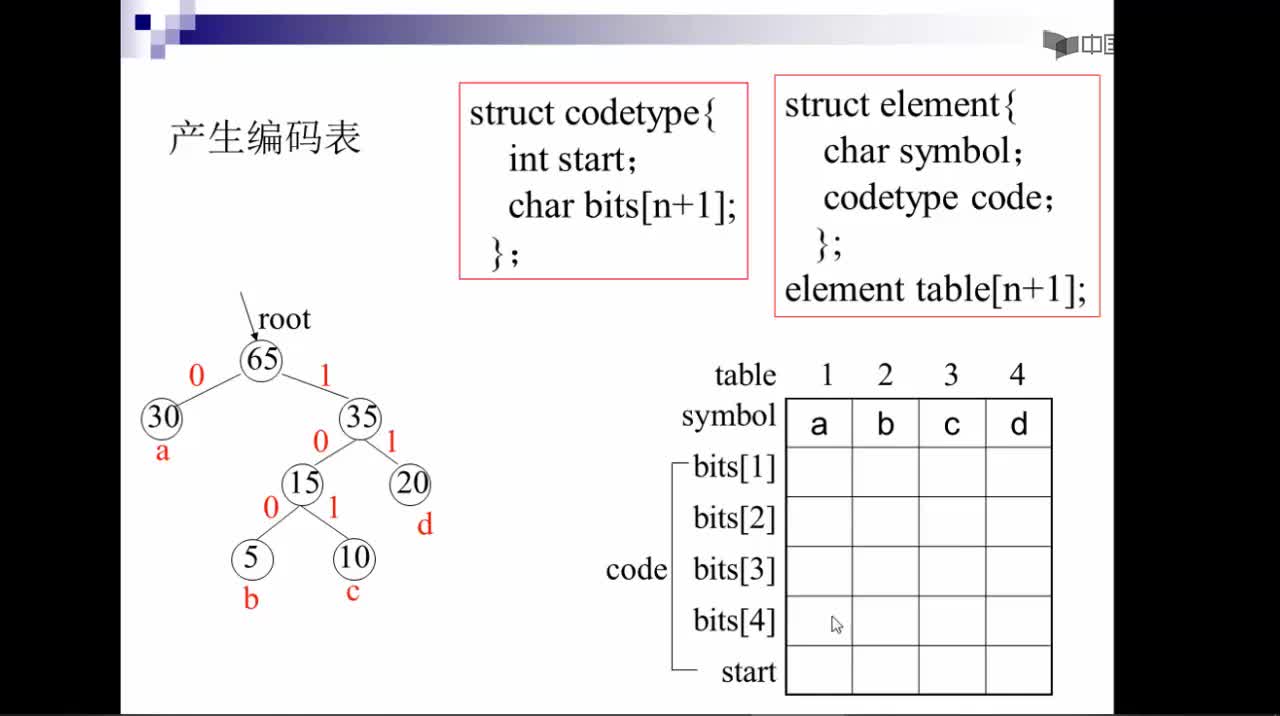
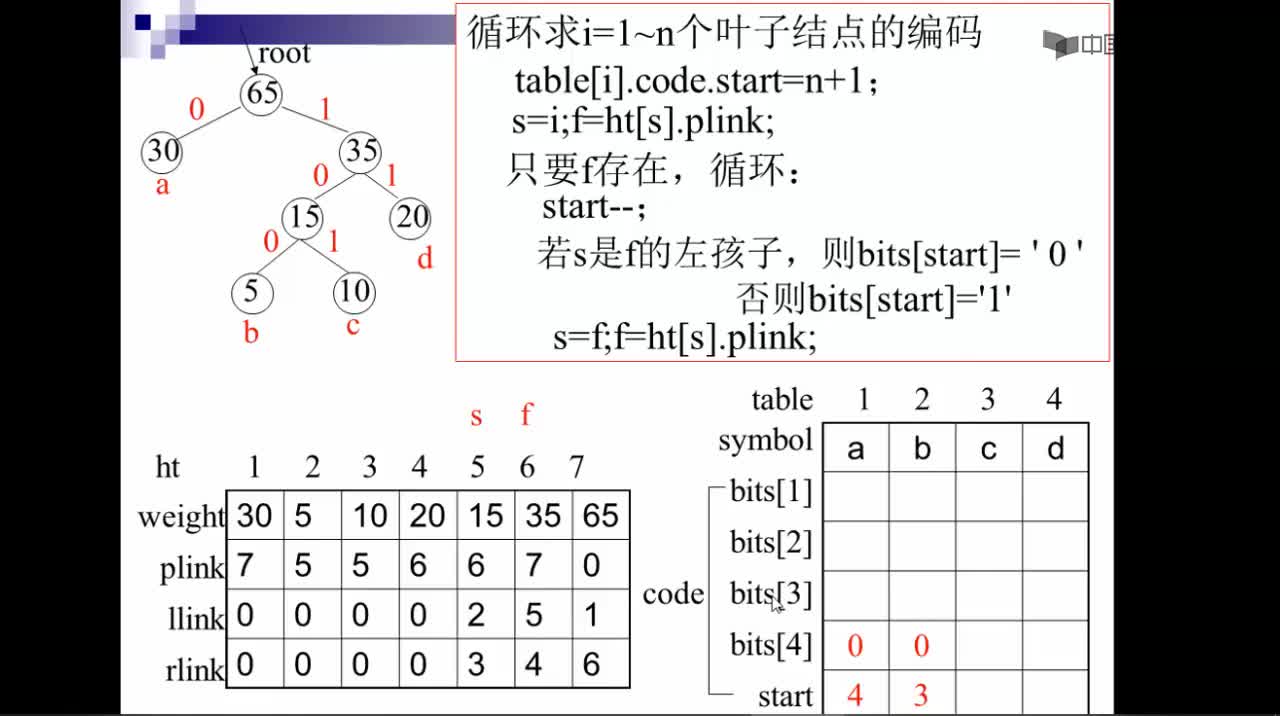
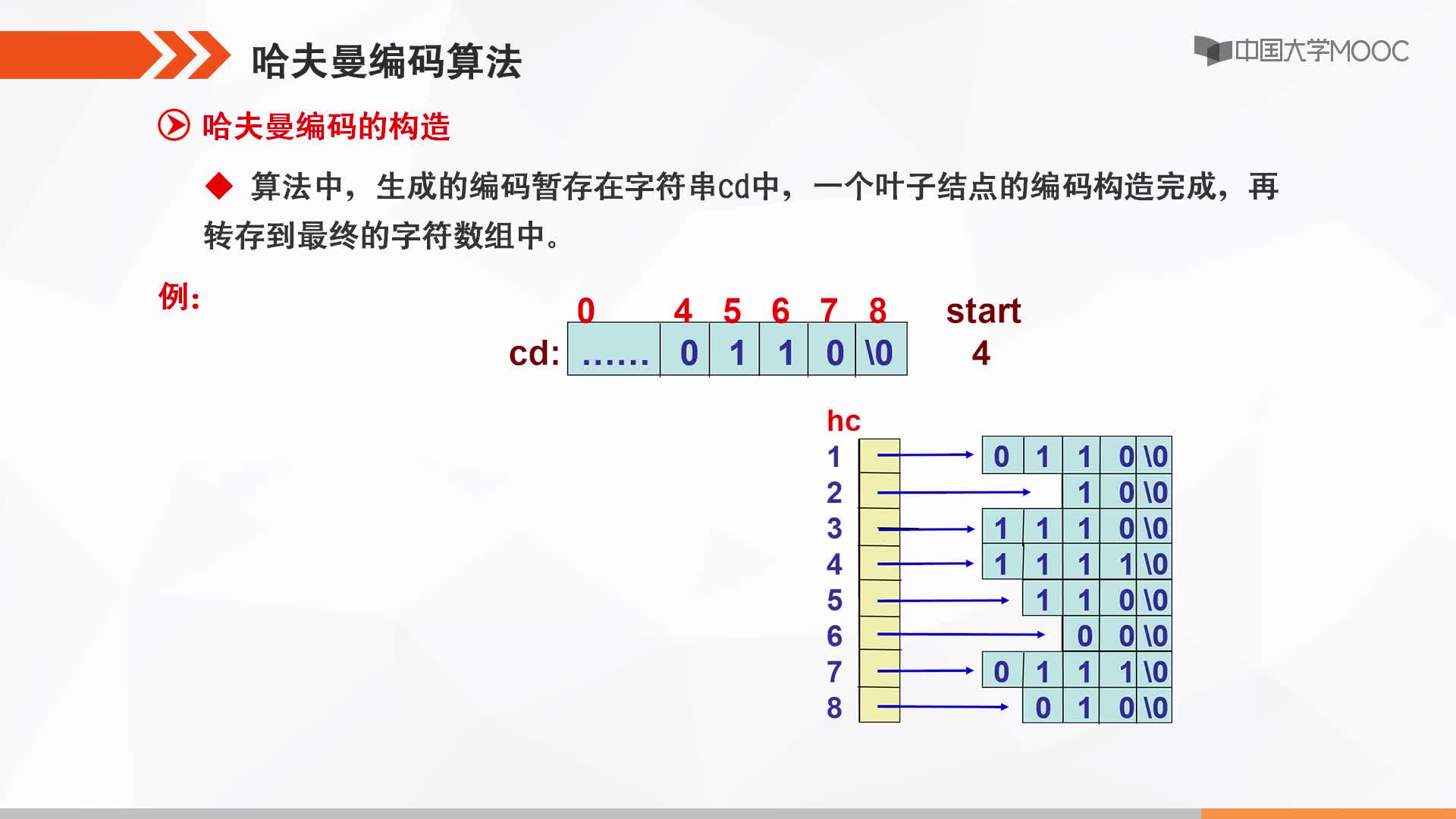
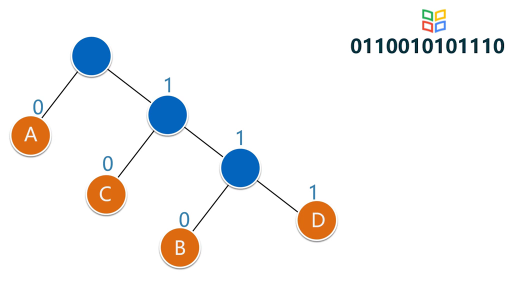
對于這個問題,可以利用哈夫曼樹加以解決:用d1,d2,d3…dn作為外部結點,用w1,w2,w3…wn作為外部結點的權,構造哈夫曼樹。在哈夫曼樹中把從每個結點引向其左子結點的邊標上二進制數“0”,把從每個結點引向右子節點的邊標上二進制數“1”,從根到每個葉結點的路徑上的二進制數連接起來,就是這個葉結點所代表字符的最優前綴編碼。通常把這種編碼稱為哈夫曼編碼。例如:
D={d1,d2,d3,d4,d5,d6,d7,d8,d9,d10,d11,d12,d13} W={2,3,5,7,11,13,17,19,23,29,31,37,41} 利用哈夫曼算法構造出如下圖所示的哈夫曼樹:

從而得到各字符的編碼為:
d1:1011110 d2:1011111
d3:101110 d4:10110
d5:0100 d6:0101
d7:1010 d8:000
d9:001 d10:011
d11:100 d12:110
d13:111
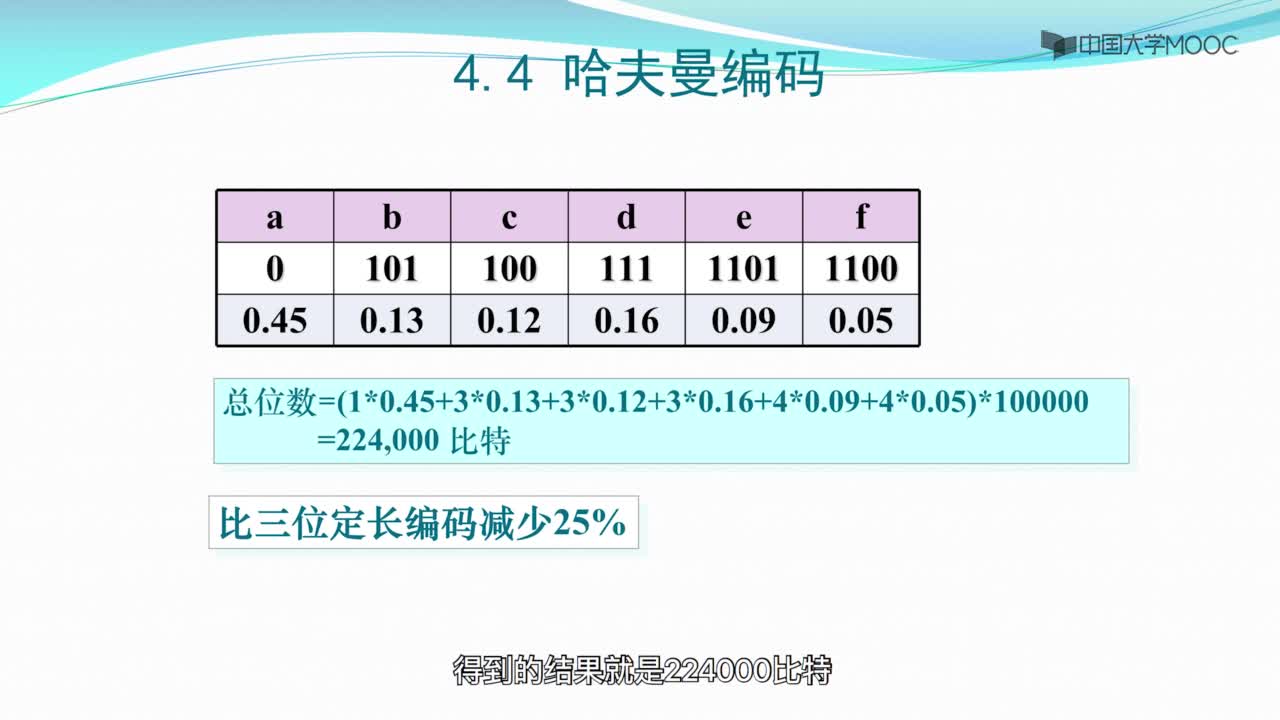
編碼的結果是,出現頻率大的字符其編碼較短,出現頻率較小的字符其編碼較長。
哈夫曼算法實現
實現的時候我們用vector《bool》記錄每個char的編碼;用map《char,vector《bool》》表示整個字典;
就得到了下面的代碼(下面有兩個,一對一錯):
先放出來這個錯的,以示警戒:
[cpp] view plain copy/************************************************************************/
/* File Name: Huffman.cpp
* @Function: Lossless Compression
@Author: Sophia Zhang
@Create Time: 2012-9-26 10:40
@Last Modify: 2012-9-26 11:10
*/
/************************************************************************/
#include“iostream”
#include “queue”
#include “map”
#include “string”
#include “iterator”
#include “vector”
#include “algorithm”
using namespace std;
#define NChar 8 //suppose use at most 8 bits to describe all symbols
#define Nsymbols 1《《NChar //can describe 256 symbols totally (include a-z, A-Z)
typedef vector《bool》 Huff_code;//8 bit code of one char
map《char,Huff_code》 Huff_Dic; //huffman coding dictionary
class HTree
{
public :
HTree* left;
HTree* right;
char ch;
int weight;
HTree(){left = right = NULL; weight=0;}
HTree(HTree* l,HTree* r,int w,char c){left = l; right = r; weight=w; ch=c;}
~HTree(){delete left; delete right;}
int Getweight(){return weight?weight:left-》weight+right-》weight;}
bool Isleaf(){return !left && !right; }
bool operator 《 (const HTree tr) const
{
return tr.weight 《 weight;
}
};
HTree* BuildTree(int *frequency)
{
priority_queue《HTree*》 QTree;
for (int i=0;i《Nsymbols;i++)
{
if(frequency[i])
QTree.push(new HTree(NULL,NULL,frequency[i],(char)i));
}
//build
while (QTree.size()》1)
{
HTree* lc = QTree.top();
QTree.pop();
HTree* rc = QTree.top();
QTree.pop();
HTree* parent = new HTree(lc,rc,parent-》Getweight(),(char)256);
QTree.push(parent);
}
//return tree root
return QTree.top();
}
void Huffman_Coding(HTree* root, Huff_code& curcode)
{
if(root-》Isleaf())
{
Huff_Dic[root-》ch] = curcode;
return;
}
Huff_code& lcode = curcode;
Huff_code& rcode = curcode;
lcode.push_back(false);
rcode.push_back(true);
Huffman_Coding(root-》left,lcode);
Huffman_Coding(root-》right,rcode);
}
int main()
{
int freq[Nsymbols] = {0};
char *str = “this is the string need to be compressed”;
//statistic character frequency
while (*str!=‘\0’)
freq[*str++]++;
//build tree
HTree* r = BuildTree(freq);
Huff_code nullcode;
nullcode.clear();
Huffman_Coding(r,nullcode);
for(map《char,Huff_code》::iterator it = Huff_Dic.begin(); it != Huff_Dic.end(); it++)
{
cout《《(*it).first《《‘\t’;
Huff_code vec_code = (*it).second;
for (vector《bool》::iterator vit = vec_code.begin(); vit!=vec_code.end();vit++)
{
cout《《(*vit)《《endl;
}
}
}
上面這段代碼,我運行出來不對。在調試的時候發現了一個問題,就是QTree優先隊列中的排序出了問題,說來也是,上面的代碼中,我重載小于號是對HTree object做的;而實際上我建樹時用的是指針,那么優先級隊列中元素為指針時該怎么辦呢?
那我們將friend bool operator 》(Node node1,Node node2)修改為friend bool operator 》(Node* node1,Node* node2),也就是傳遞的是Node的指針行不行呢?
答案是不可以,因為根據c++primer中重載操作符中講的“程序員只能為類類型或枚舉類型的操作數定義重載操作符,在把操作符聲明為類的成員時,至少有一個類或枚舉類型的參數按照值或者引用的方式傳遞”,也就是說friend bool operator 》(Node* node1,Node* node2)形參中都是指針類型的是不可以的。我們只能再建一個類,用其中的重載()操作符作為優先隊列的比較函數。
就得到了下面正確的代碼:
[cpp] view plain copy/************************************************************************/
/* File Name: Huffman.cpp
* @Function: Lossless Compression
@Author: Sophia Zhang
@Create Time: 2012-9-26 10:40
@Last Modify: 2012-9-26 12:10
*/
/************************************************************************/
#include“iostream”
#include “queue”
#include “map”
#include “string”
#include “iterator”
#include “vector”
#include “algorithm”
using namespace std;
#define NChar 8 //suppose use 8 bits to describe all symbols
#define Nsymbols 1《《NChar //can describe 256 symbols totally (include a-z, A-Z)
typedef vector《bool》 Huff_code;//8 bit code of one char
map《char,Huff_code》 Huff_Dic; //huffman coding dictionary
/************************************************************************/
/* Tree Class elements:
*2 child trees
*character and frequency of current node
*/
/************************************************************************/
class HTree
{
public :
HTree* left;
HTree* right;
char ch;
int weight;
HTree(){left = right = NULL; weight=0;ch =‘\0’;}
HTree(HTree* l,HTree* r,int w,char c){left = l; right = r; weight=w; ch=c;}
~HTree(){delete left; delete right;}
bool Isleaf(){return !left && !right; }
};
/************************************************************************/
/* prepare for pointer sorting*/
/*because we cannot use overloading in class HTree directly*/
/************************************************************************/
class Compare_tree
{
public:
bool operator () (HTree* t1, HTree* t2)
{
return t1-》weight》 t2-》weight;
}
};
/************************************************************************/
/* use priority queue to build huffman tree*/
/************************************************************************/
HTree* BuildTree(int *frequency)
{
priority_queue《HTree*,vector《HTree*》,Compare_tree》 QTree;
//1st level add characters
for (int i=0;i《Nsymbols;i++)
{
if(frequency[i])
QTree.push(new HTree(NULL,NULL,frequency[i],(char)i));
}
//build
while (QTree.size()》1)
{
HTree* lc = QTree.top();
QTree.pop();
HTree* rc = QTree.top();
QTree.pop();
HTree* parent = new HTree(lc,rc,lc-》weight+rc-》weight,(char)256);
QTree.push(parent);
}
//return tree root
return QTree.top();
}
/************************************************************************/
/* Give Huffman Coding to the Huffman Tree*/
/************************************************************************/
void Huffman_Coding(HTree* root, Huff_code& curcode)
{
if(root-》Isleaf())
{
Huff_Dic[root-》ch] = curcode;
return;
}
Huff_code lcode = curcode;
Huff_code rcode = curcode;
lcode.push_back(false);
rcode.push_back(true);
Huffman_Coding(root-》left,lcode);
Huffman_Coding(root-》right,rcode);
}
int main()
{
int freq[Nsymbols] = {0};
char *str = “this is the string need to be compressed”;
//statistic character frequency
while (*str!=‘\0’)
freq[*str++]++;
//build tree
HTree* r = BuildTree(freq);
Huff_code nullcode;
nullcode.clear();
Huffman_Coding(r,nullcode);
for(map《char,Huff_code》::iterator it = Huff_Dic.begin(); it != Huff_Dic.end(); it++)
{
cout《《(*it).first《《‘\t’;
std::copy(it-》second.begin(),it-》second.end(),std::ostream_iterator《bool》(cout));
cout《《endl;
}
}
 電子發燒友App
電子發燒友App


































































評論