一、引言

　　DFT（離散傅里葉變換）作為將信號從時域轉(zhuǎn)換到頻域的基本運算，在各種數(shù)字信號處理中起著核心作用，其快速算法FFT（快速傅里葉變換）在無線通信、語音識別、圖像處理和頻譜分析等領(lǐng)域有著廣泛的應(yīng)用。用大規(guī)模集成電路FPGA（現(xiàn)場可編程門陣列）來實現(xiàn)FFT算法時，需要重點考慮的不再是算法運算量，而是算法的復(fù)雜性、規(guī)整性和模塊化，因為算法的簡單性和規(guī)整性將更適合大規(guī)模集成，更方便于版圖設(shè)計，而算法的模塊化更有利于FFT處理器的靈活擴展。組合數(shù)FFT算法和CORDIC（坐標(biāo)旋轉(zhuǎn)數(shù)字計算機）算法結(jié)合起來，在計算長點數(shù)、可擴展FFT時具有較大的優(yōu)越性［1，2］。而面向高速、大容量數(shù)據(jù)流的FFT的實時處理，可以通過VLSI（超大規(guī)模集成電路）器件的并行處理或多級流水線處理等來達到。特別是多級流水線處理的FFT結(jié)構(gòu)使得基于FPGA器件的FFT處理器完成不同點數(shù)的FFT計算時可以通過增減模塊級數(shù)很容易地實現(xiàn)。

　　二、組合數(shù)N=r1r2點混合基FFT原理

　　計算N點DFT：

　　式中k=0，1，…，N-1。

　　若N=r1r2的組合數(shù)，可將n（n＜N）表示為

　　式（2）的意

　　義在于，計算組合數(shù)N=r1r2點DFT，等價于先求出r?2組r?1點的DFT，其結(jié)果經(jīng)過對應(yīng)旋轉(zhuǎn)因子的相位旋轉(zhuǎn)后，再計算r1組r2點的DFT。實際應(yīng)用中，DFT往往用它的快速算法FFT實現(xiàn)，因而式（2）中的r1點DFT和r2點DFT都用r1點FFT和r2點FFT實現(xiàn)。

　　三、可擴展FFT處理器實現(xiàn)結(jié)構(gòu)

　　根據(jù)式（2）的FFT算法原理設(shè)計FFT處理器的可擴展結(jié)構(gòu)如圖1所示。

　　采用流水線模塊化級聯(lián)結(jié)構(gòu)，把FFT處理器劃分成短點數(shù)FFT、級間混序RAM和相位旋轉(zhuǎn)等功能模塊，設(shè)計的各功能模塊可以重復(fù)利用，通過復(fù)用或增減各功能模塊可以靈活改變FFT處理器的計算規(guī)模，而且不增加設(shè)計量。在圖1結(jié)構(gòu)中，當(dāng)Li＝1時，就演變成了基2 FFT；當(dāng)Li＝2時，就演變成了基4 FFT；同理，當(dāng)Li≠Lj時，就演變成了高組合數(shù)的混合基FFT。

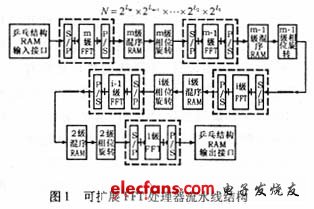
　　1.短點數(shù)FFT陣列結(jié)構(gòu)

　　－Tukey算法結(jié)構(gòu)實現(xiàn)時，有大量的復(fù)數(shù)乘法實際上轉(zhuǎn)化為加減運算，所以用陣列結(jié)構(gòu)實現(xiàn)不但具有速度快的優(yōu)點，而且所用器件資源也減少很多，通過對陣列結(jié)構(gòu)短點數(shù)FFT進行時分復(fù)用，可以提高運算單元的使用效率。

　　2.相位旋轉(zhuǎn)運算單元

　　實現(xiàn)短點數(shù)FFT級間相位旋轉(zhuǎn)，采用ROM存儲旋轉(zhuǎn)因子與數(shù)據(jù)復(fù)乘的傳統(tǒng)方法，不僅涉及乘法運算，而且會消耗大量存儲器資源。

　　利用CORDIC算法實現(xiàn)組合數(shù)FFT級間數(shù)據(jù)的相位旋轉(zhuǎn)，把乘法轉(zhuǎn)化成加減法運算，適合FPGA的大規(guī)模集成。可以設(shè)計出統(tǒng)一結(jié)構(gòu)的CORDIC處理器模塊，重復(fù)利用于不同級間實現(xiàn)相位旋轉(zhuǎn)，而且其控制邏輯非常簡單。

　　（1）CORDIC算法原理

　　如果旋轉(zhuǎn)角度θ可以分解成n個小角度φi之和，即：

　　公式：

　　（2）CORDIC處理器結(jié)構(gòu)設(shè)計

　　本文提出了一種流水線CORDIC處理器結(jié)構(gòu)的解決方案。實現(xiàn)式子（4）的迭代運算時采用補碼移位和補碼加減運算，可以減少大量求補運算，其迭代結(jié)構(gòu)如圖2所示。

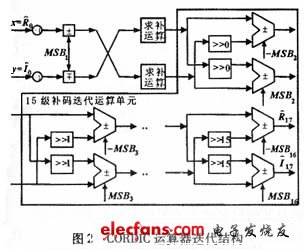
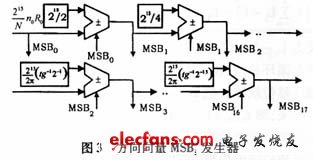
　　前者在于左移補零的位數(shù)的不同，這樣，只需要改變n0k0的放大倍數(shù)（改變左移低位補零的位數(shù)），就可以把同一方向向量功能模塊級聯(lián)到圖1 FFT處理器的不同級間來計算CORDIC處理器的MSBi，這就大大地減小了重復(fù)設(shè)計，其迭代結(jié)構(gòu)如圖3所示。